Average velocity of a particle executing SHM in one complete vibration is :
zero
Aω2
Aω
Aω22
The correct Answer is:A
To find the average velocity of a particle executing Simple Harmonic Motion (SHM) in one complete vibration, we can follow these steps:
1. Understanding SHM: A particle in SHM moves back and forth around an equilibrium position. In one complete vibration, the particle moves from one extreme position to the other and then returns to the starting point.
2. Displacement Calculation: Displacement is defined as the change in position of the particle. In one complete vibration, the particle starts from an extreme position, moves to the opposite extreme, and then returns to the original position. Therefore, the initial and final positions are the same.
3. Displacement Value: Since the particle returns to its starting point after one complete vibration, the total displacement is:
Displacement=Final Position−Initial Position=0−0=0
4. Time Calculation: Let T be the time taken for one complete vibration (one complete oscillation).
5. Average Velocity Formula: Average velocity is defined as:
Average Velocity=DisplacementTime=0T=0
6. Conclusion: Therefore, the average velocity of a particle executing SHM in one complete vibration is:
Average Velocity=0
Final Answer:
The average velocity of a particle executing SHM in one complete vibration is 0.
Displacement=Final Position−Initial Position=0−0=0
Average Velocity=DisplacementTime=0T=0
Average Velocity=0
The average velocity of a particle executing SHM in one complete vibration is 0.
Similar Questions
Knowledge Check
When the displacement of a particle executing SHM is one-fourth of its amplitude, what fraction of the total energy is the kinetic energy?
A1615B1516C34D43
The maximum velocity of a particle, executing SHM with an amplitude 7 mm is 4.4 m/s. the period of oscillation is
View Solution
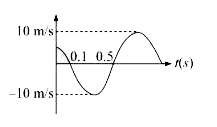
The variation of velocity of a particle executing SHM with time is shown is fig. The velocity of the particle when a phase change of π6 takes place from the instant it is at one of the extreme positions will be
View SolutionThe velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
View SolutionIf the displacement (x) and velocity (v) of a particle executing SHM are related through the expression 3v2=30−x2. If the time period of the particle is T=π√n, then what is the value of n?
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
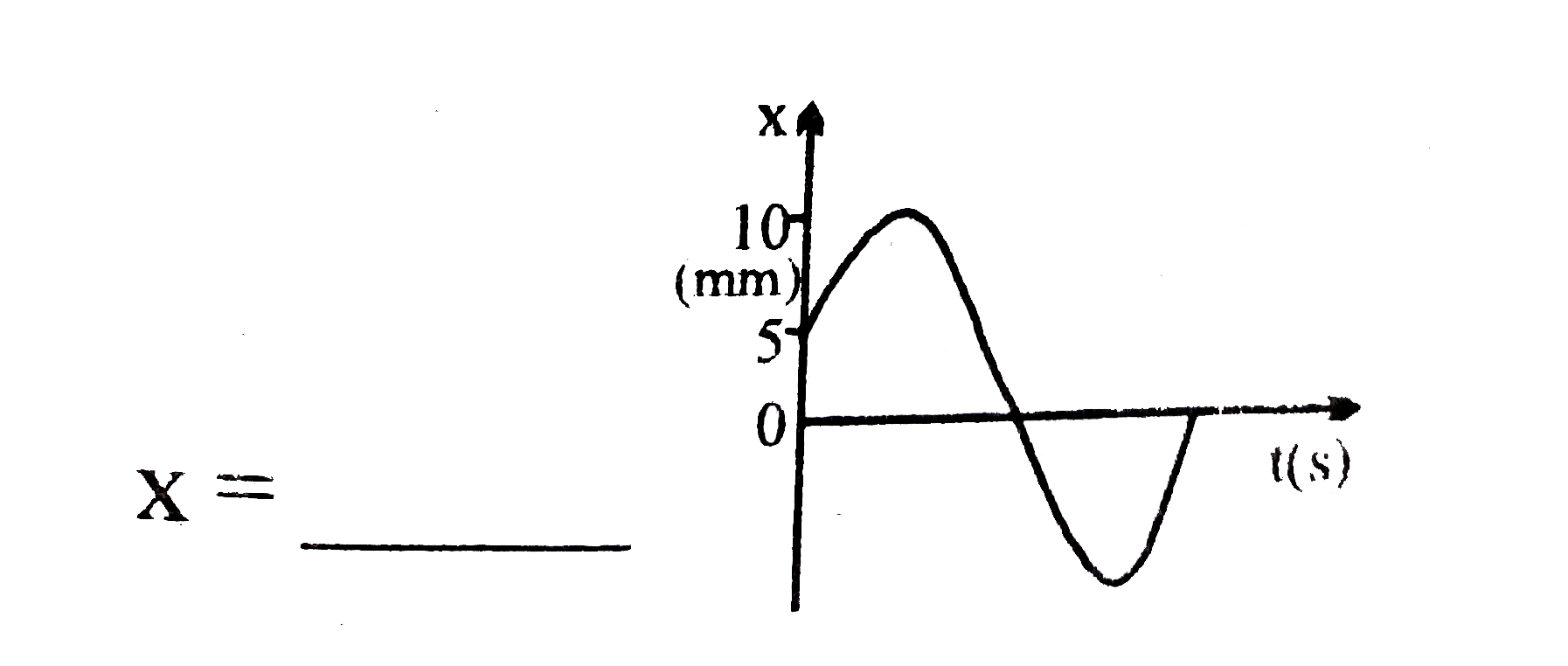
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
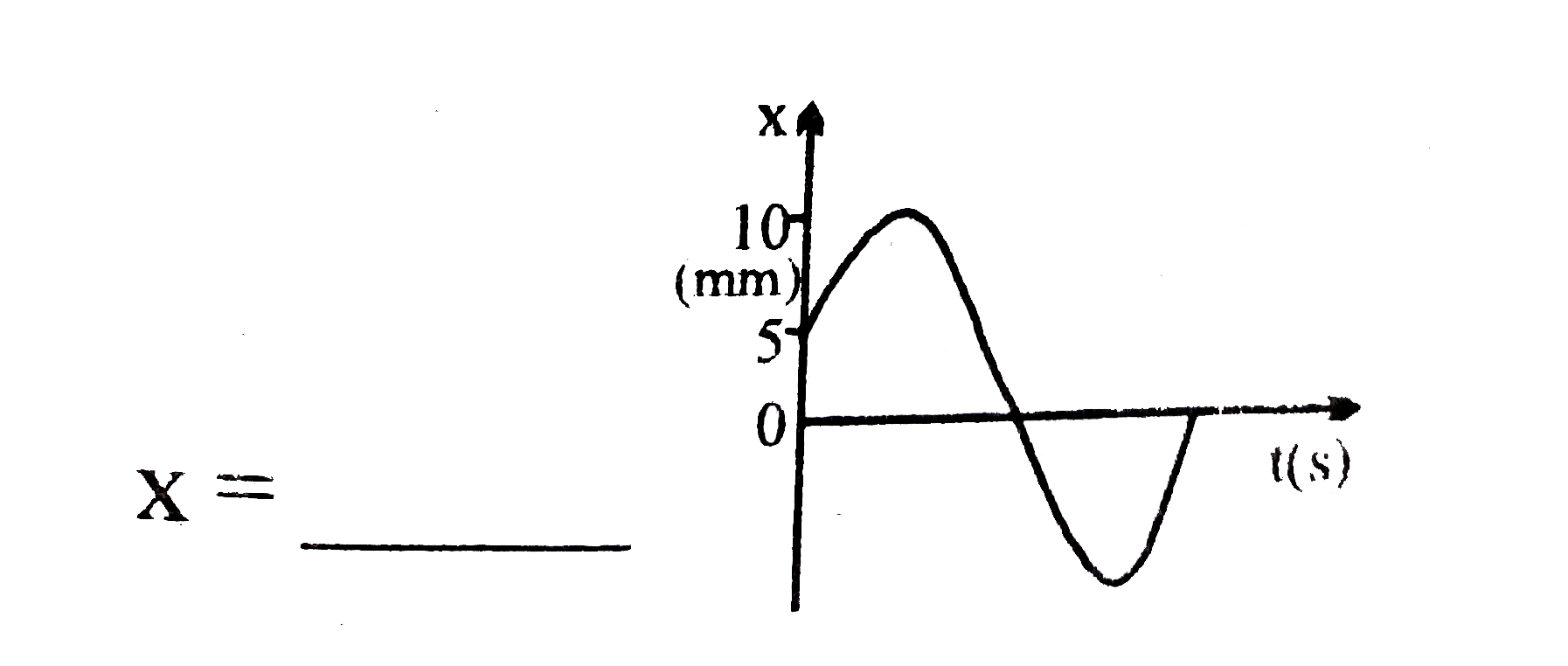
View SolutionVelocity at mean position of a particle executing SHM is v. Velocity of the particle at a distance equal to half of the amplitude will be
View Solution
