A piece of wax floats in brine. What fraction of its volume will be immersed?
Density of wax = 0.95 g cm−3 ,
Density of brine = 1.1 g cm−3.
To find the fraction of the volume of wax that is immersed in brine, we can use the principle of flotation, which states that the weight of the object (in this case, the wax) is equal to the weight of the fluid it displaces (the brine).
1. Identify the given data:
- Density of wax (ρwax) = 0.95 g/cm³
- Density of brine (ρbrine) = 1.1 g/cm³
2. Let the total volume of the wax be V1 cm³.
- The volume of wax that is immersed in brine is V2 cm³.
3. Calculate the mass of the wax:
- The mass of the wax can be calculated using the formula:
Mass of wax=Volume×Density=V1×0.95 g
4. Calculate the weight of the wax:
- The weight of the wax is given by:
Weight of wax=Mass×g=(V1×0.95)×g
5. Calculate the mass of the brine displaced:
- The mass of the brine displaced when the wax is submerged is:
Mass of brine displaced=V2×ρbrine=V2×1.1 g
6. Calculate the weight of the brine displaced:
- The weight of the brine displaced is:
Weight of brine displaced=Mass×g=(V2×1.1)×g
7. Apply the principle of flotation:
- According to the principle of flotation:
Weight of wax=Weight of brine displaced
- Therefore, we can set up the equation:
(V1×0.95)×g=(V2×1.1)×g
8. Cancel g from both sides:
- This simplifies to:
V1×0.95=V2×1.1
9. Rearranging the equation to find the fraction V2V1:
- Dividing both sides by V1 and rearranging gives:
V2V1=0.951.1
10. Calculate the fraction:
- Now, calculate 0.951.1:
0.951.1≈0.8636
- Therefore, approximately 0.86 (or 86%) of the volume of the wax is immersed in brine.
Final Answer:
The fraction of the volume of wax that is immersed in brine is approximately 0.86.
- Density of wax (ρwax) = 0.95 g/cm³
- Density of brine (ρbrine) = 1.1 g/cm³
- The volume of wax that is immersed in brine is V2 cm³.
- The mass of the wax can be calculated using the formula:
Mass of wax=Volume×Density=V1×0.95 g
- The weight of the wax is given by:
Weight of wax=Mass×g=(V1×0.95)×g
- The mass of the brine displaced when the wax is submerged is:
Mass of brine displaced=V2×ρbrine=V2×1.1 g
- The weight of the brine displaced is:
Weight of brine displaced=Mass×g=(V2×1.1)×g
- According to the principle of flotation:
Weight of wax=Weight of brine displaced
- Therefore, we can set up the equation:
(V1×0.95)×g=(V2×1.1)×g
- This simplifies to:
V1×0.95=V2×1.1
- Dividing both sides by V1 and rearranging gives:
V2V1=0.951.1
- Now, calculate 0.951.1:
0.951.1≈0.8636
- Therefore, approximately 0.86 (or 86%) of the volume of the wax is immersed in brine.
The fraction of the volume of wax that is immersed in brine is approximately 0.86.
Topper's Solved these Questions
- FLUIDSBook:ICSEChapter:FLUIDSExercise:TOPIC 2 (3 Marks Questions )
Explore 23 Videos
- FLUIDSBook:ICSEChapter:FLUIDSExercise:TOPIC 2 (4 Marks Questions )
Explore 16 Videos
- FLUIDSBook:ICSEChapter:FLUIDSExercise:TOPIC 1 (4 Marks Questions )
Explore 10 Videos
- ELECTRICITY AND MAGNETISM Book:ICSEChapter:ELECTRICITY AND MAGNETISM Exercise:TOPIC 2 Magnetism (4 Marks Questions )
Explore 6 Videos
- HEAT AND ENERGYBook:ICSEChapter:HEAT AND ENERGYExercise:EXERCISE -6(D) Multiple Choice Question)
Explore 4 Videos
Similar Questions
Knowledge Check
Iceberg floats in sea water with a part of it submerged. The percentage fraction of the ice berg not submerged is (density of ice = 0.9gcm−3, density of sea water = 1.1gcm−3)
A18%B12%C10%D8%
Iceberg floats in water with part of it submerged. What is the fraction of the volume of iceberg submerged if the density of ice is ρi=0.917gcm−3?
View SolutionWhat is the volume of one molecules of water (density of H2O=1gcm−3)
View Solution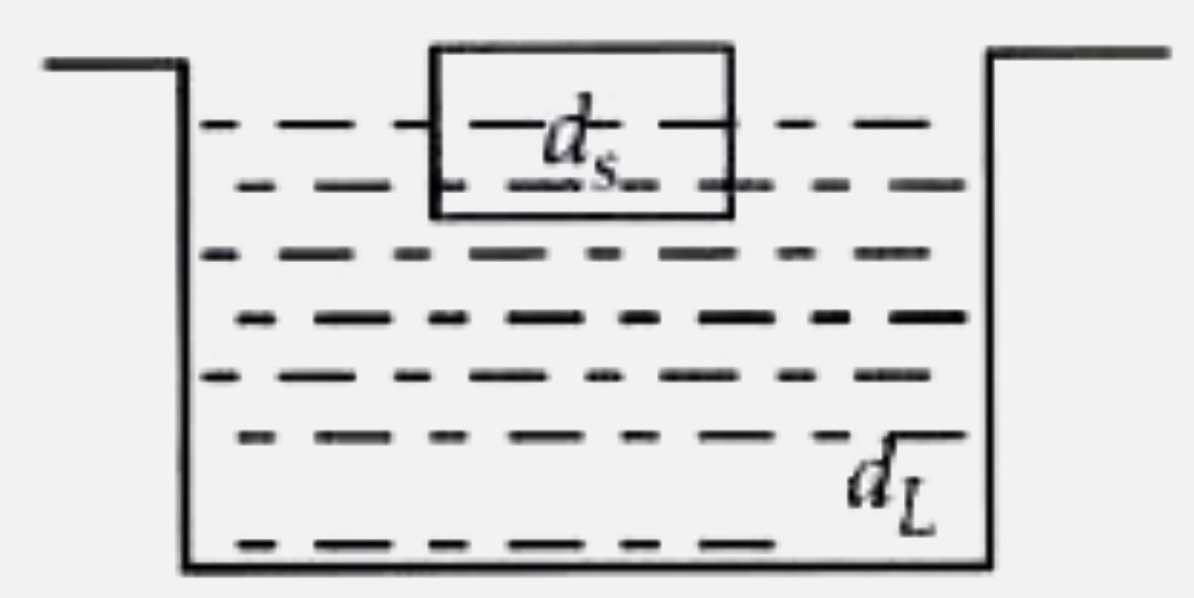
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )
View SolutionA cube is floating on mercury with (1/5)th of its volume submerged. If suficient water Is added to cover the cube, what fraction of its volume will remain immersed in mercury ? Density of mercury = 13600kg/m3.
View SolutionThe density of a substance in 0.9g/cm3
Find its density in SI units.
View SolutionIf the density of wood is 0.6 g/cm3 , what is the mass of 10cm3 ?
View SolutionA piece of iron (density 7.6 g cm−3 ) sinks in mercury (density 13.6g cm−3 ).
View Solution

