A vessel of base area 100 cm x 60 cm and height 200 cm is completely filled with a liquid of density 1.1×103kgm−3 Ignoring the atmosphere pressure find the thrust at the bottom of the vessel
To solve the problem of finding the thrust at the bottom of the vessel filled with liquid, we can follow these steps:
Step 1: Convert the dimensions of the vessel to standard units
The base area of the vessel is given in centimeters. We need to convert these measurements to meters.
- Base area dimensions:
- Length = 100 cm = 100 / 100 = 1 m
- Width = 60 cm = 60 / 100 = 0.6 m
Step 2: Calculate the area of the base of the vessel
The area A of the base of the vessel can be calculated using the formula:
A=Length×Width
Substituting the values:
A=1m×0.6m=0.6m2
Step 3: Calculate the volume of the vessel
The height of the vessel is also given in centimeters, which we need to convert to meters.
- Height = 200 cm = 200 / 100 = 2 m
The volume V of the vessel can be calculated using the formula:
V=A×Height
Substituting the values:
V=0.6m2×2m=1.2m3
Step 4: Calculate the mass of the liquid
The mass m of the liquid can be calculated using the formula:
m=Density×Volume
The density of the liquid is given as 1.1×103kg/m3. Thus,
m=1.1×103kg/m3×1.2m3=1320kg
Step 5: Calculate the weight of the liquid
The weight W of the liquid can be calculated using the formula:
W=m×g
where g (acceleration due to gravity) is approximately 9.8m/s2. Thus,
W=1320kg×9.8m/s2=12936N
Step 6: Conclude with the thrust at the bottom of the vessel
Since the thrust at the bottom of the vessel is equal to the weight of the liquid, we can conclude that:
Thrust=12936N≈1.294×104N
Final Answer:
The thrust at the bottom of the vessel is approximately 1.294×104N.
---
The base area of the vessel is given in centimeters. We need to convert these measurements to meters.
- Length = 100 cm = 100 / 100 = 1 m
- Width = 60 cm = 60 / 100 = 0.6 m
The area A of the base of the vessel can be calculated using the formula:
A=Length×Width
Substituting the values:
A=1m×0.6m=0.6m2
The height of the vessel is also given in centimeters, which we need to convert to meters.
- Height = 200 cm = 200 / 100 = 2 m
V=A×Height
Substituting the values:
V=0.6m2×2m=1.2m3
The mass m of the liquid can be calculated using the formula:
m=Density×Volume
The density of the liquid is given as 1.1×103kg/m3. Thus,
m=1.1×103kg/m3×1.2m3=1320kg
The weight W of the liquid can be calculated using the formula:
W=m×g
where g (acceleration due to gravity) is approximately 9.8m/s2. Thus,
W=1320kg×9.8m/s2=12936N
Since the thrust at the bottom of the vessel is equal to the weight of the liquid, we can conclude that:
Thrust=12936N≈1.294×104N
The thrust at the bottom of the vessel is approximately 1.294×104N.
Topper's Solved these Questions
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (2 Marks Questions )
45 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (3 Marks Questions )
23 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 1 (3 Marks Questions )
18 Videos
- ELECTRICITY AND MAGNETISM BOOK - ICSECHAPTER - ELECTRICITY AND MAGNETISM EXERCISE - TOPIC 2 Magnetism (4 Marks Questions )
6 Videos
- HEAT AND ENERGYBOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)
4 Videos
Similar Questions
A vessel of base area 100 cm x 60 cm and height 200 cm is completely filled with a liquid of density 1.1×103kgm−3 Ignoring the atmosphere pressure find the pressure at the depth of 5 cm from the free surface
View SolutionA vessel of base area 100cm×60cm and height 200cm is completely filled with a liquid of density 1.1×103kgm−3.
(a) Ignoring the atmospheric pressure, find :
(i) the thrust at the bottom of the vessel,
(ii) the pressure at the bottom of the vessel,
(iii) The pressure at a depth of 5 cm from the free surface,
(iv) the net force experienced by a metal foil of area 10cm2 placed at a depth of 5 cm from the free surface,
(b) The thrust at the bottom of the vessel if the atmospheric pressure equal to 1×105Nm−2 is taken into account.
Take g=9.8ms−2 .
View SolutionA body is volume 100cm3 weighs 5 kgf in air. It is completely immersed in a liquid of density 1.8×103kgm−3. Find (i) the upthrust due to liquid and (ii) the weight of the body in liquid.
View SolutionA vessel of length l, breadth b and height h is filled completely with a liquid of density d (see figure) Calculate the thrust on each surface of the cube.
View SolutionA person just observes the point A on the circumference at the bottom of an empty cylindricla vessel of diameter 10 cm . When the vessel is completely filled with a liquid (μ=√2), he can just see the centre B of the bottom. Then the height of the vessel is

View SolutionA cube (side =10cm) of density 0.5g/cm3 is placed in a vessel of base area 20cm×20cm. A liquid of density 1.0gcm2 is gradually filled in the vessel at a constant rate Q=50cm3/s

If we plot a graph between the normal reaction on cube by the vessel versus time. The graph will be like
View SolutionIn Fig. 4.10, a tube of length 200 cm filled with a liquid of density 0.90×103kgm−3 is placed inclined with the vertical such that the level A of liquid in the tube is at a vertical height 100 cm from its lowest point C. there is a point B in the tube below the point A at a vertical depth 60cm.
(a) Calculate the pressure at points
(i) A,
(ii) B and
(iii) C
(b) What will be the pressure at point C when the tube is made vertical ?
Take atmospheric pressure =1.013×105Nm−2
View SolutionA cube (side =10cm) of density 0.5g/cm3 is placed in a vessel of base area 20cm×20cm. A liquid of density 1.0g/cm3 is gradually filled in the vessel at a constant rate Q=50cm3/s
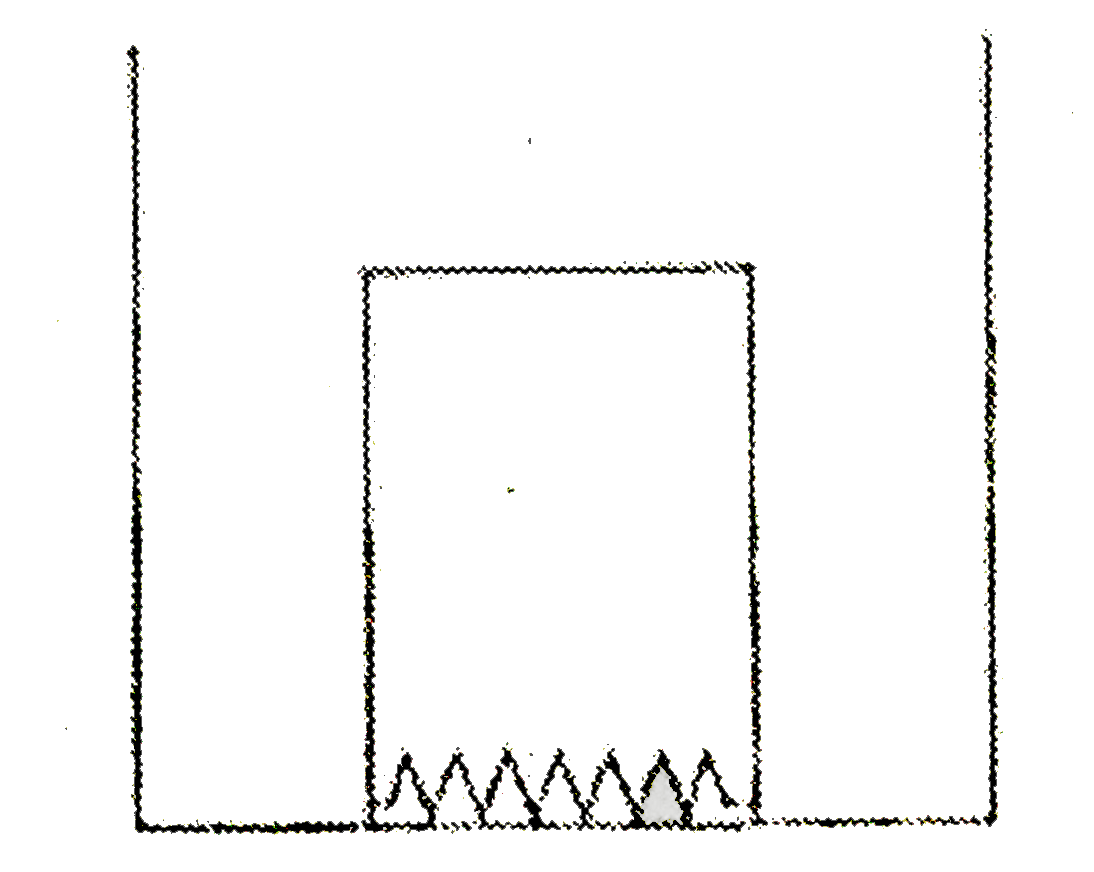
The cube will leave contact with the vessel after time t= ......... s.
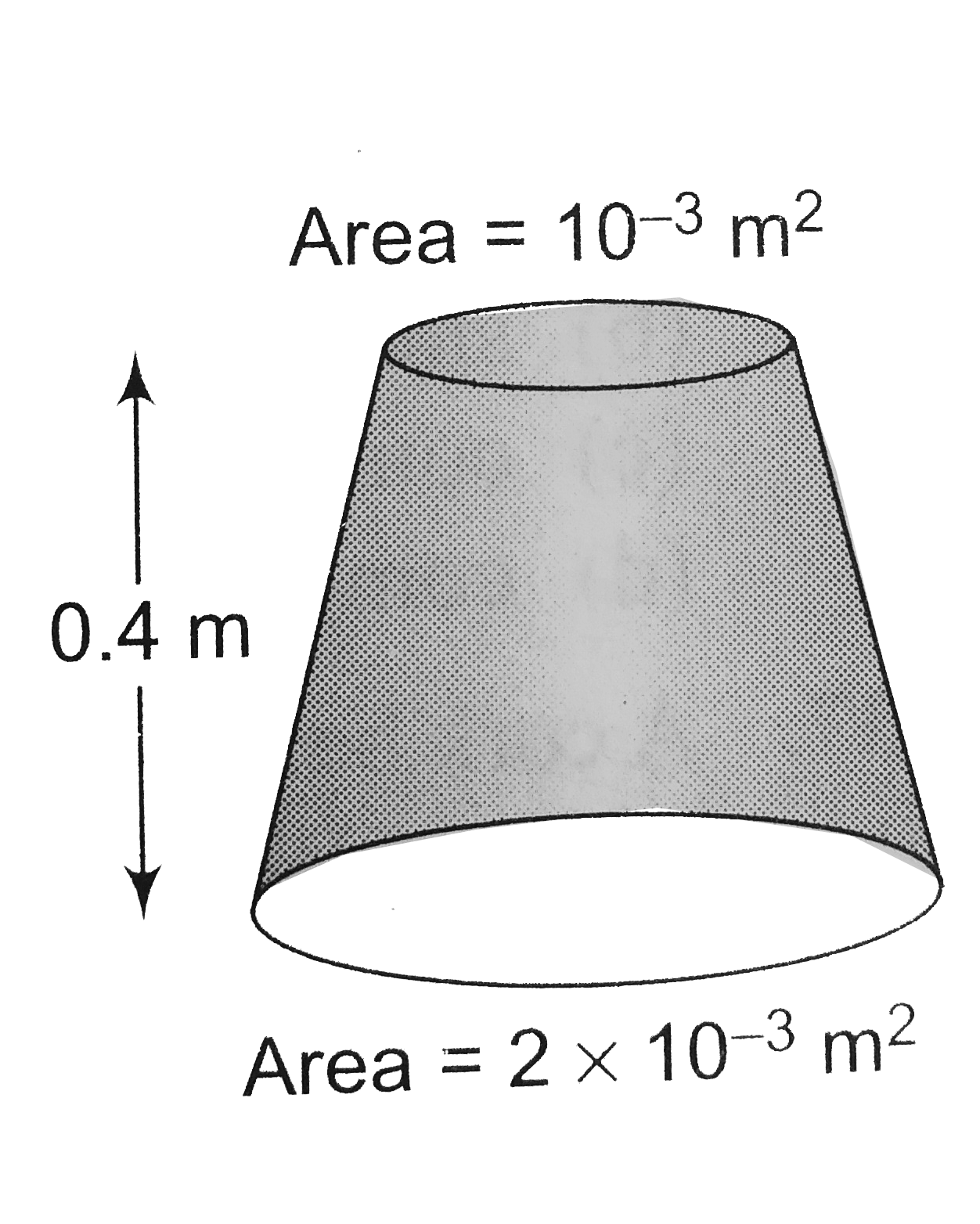
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
View SolutionTwo cylindrical vessels are filled with oil. Their radii are 15 cm, 12 cm and heights 20 cm, 16 cm respectively. Find the radius of a cylindrical vessel 21 cm in height, which will just contain the oil of the two given vessels.
View Solution
