A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the initial velocity of the ball
To find the initial velocity of a ball thrown vertically upwards that reaches a height of 20 m before returning to the ground, we can use the third equation of motion. Here’s a step-by-step solution:
Step 1: Identify the known values
- Maximum height (h) = 20 m
- Acceleration due to gravity (g) = 10 m/s² (acting downwards)
- Final velocity (v) at the maximum height = 0 m/s (the ball stops momentarily at the highest point)
Step 2: Write the third equation of motion
The third equation of motion is:
v2=u2+2as
Where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = displacement
Step 3: Substitute the known values into the equation
Since the ball is moving upwards against gravity, we take acceleration a as −g. Therefore, we can rewrite the equation as:
0=u2−2gh
Step 4: Rearrange the equation to solve for initial velocity (u)
Rearranging the equation gives:
u2=2gh
Step 5: Substitute the values of g and h
Now substituting the values of g and h:
u2=2×10m/s2×20m
u2=400
Step 6: Calculate the initial velocity (u)
Taking the square root of both sides:
u=√400
u=20m/s
Final Answer
The initial velocity of the ball is 20m/s.
---
- Maximum height (h) = 20 m
- Acceleration due to gravity (g) = 10 m/s² (acting downwards)
- Final velocity (v) at the maximum height = 0 m/s (the ball stops momentarily at the highest point)
The third equation of motion is:
v2=u2+2as
Where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = displacement
Since the ball is moving upwards against gravity, we take acceleration a as −g. Therefore, we can rewrite the equation as:
0=u2−2gh
Rearranging the equation gives:
u2=2gh
Now substituting the values of g and h:
u2=2×10m/s2×20m
u2=400
Taking the square root of both sides:
u=√400
u=20m/s
The initial velocity of the ball is 20m/s.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXAMPLES
24 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(A)
19 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 3 (3 Marks Questions )
7 Videos
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- LIGHTBOOK - ICSECHAPTER - LIGHTEXERCISE - TOPIC 2 Spherical Mirrors (4 Marks Questions )
9 Videos
Similar Questions
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the final velocity of ball on reaching the ground
View SolutionA ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the total time of journey of ball.
View SolutionA ball is thrown vertically upwards. It goes to a height 19.6 m and then comes back to the ground, Find the initial velocity of the ball .
Take g = 9.8 ms−2
View SolutionA ball is thrown vertically upwards. It goes to a height 19.6 m and then comes back to the ground, Find the final velocity of the ball when it strikes the ground.
Take g = 9.8 ms−2
View SolutionA ball is thrown vertically upwards. It returns 6 s later. Calculate the greatest height reached by the ball
View SolutionA ball is thrown vertically upwards. It was observed at a height h twice after a time interval Δt. The initial velocity of the ball is
View SolutionA ball is thrown vertically upwards with a velocity of 10 ms−1. It returns to the ground with a velocity of 9 ms−1. If g=9.8 ms−2 , then the maximum height attained by the ball is nearly (assume air resistance to be uniform)
View SolutionA ball of mass m is thrown straight up. It goes to a maximum height and then returns. Finally it strikes ground. In the whole process.
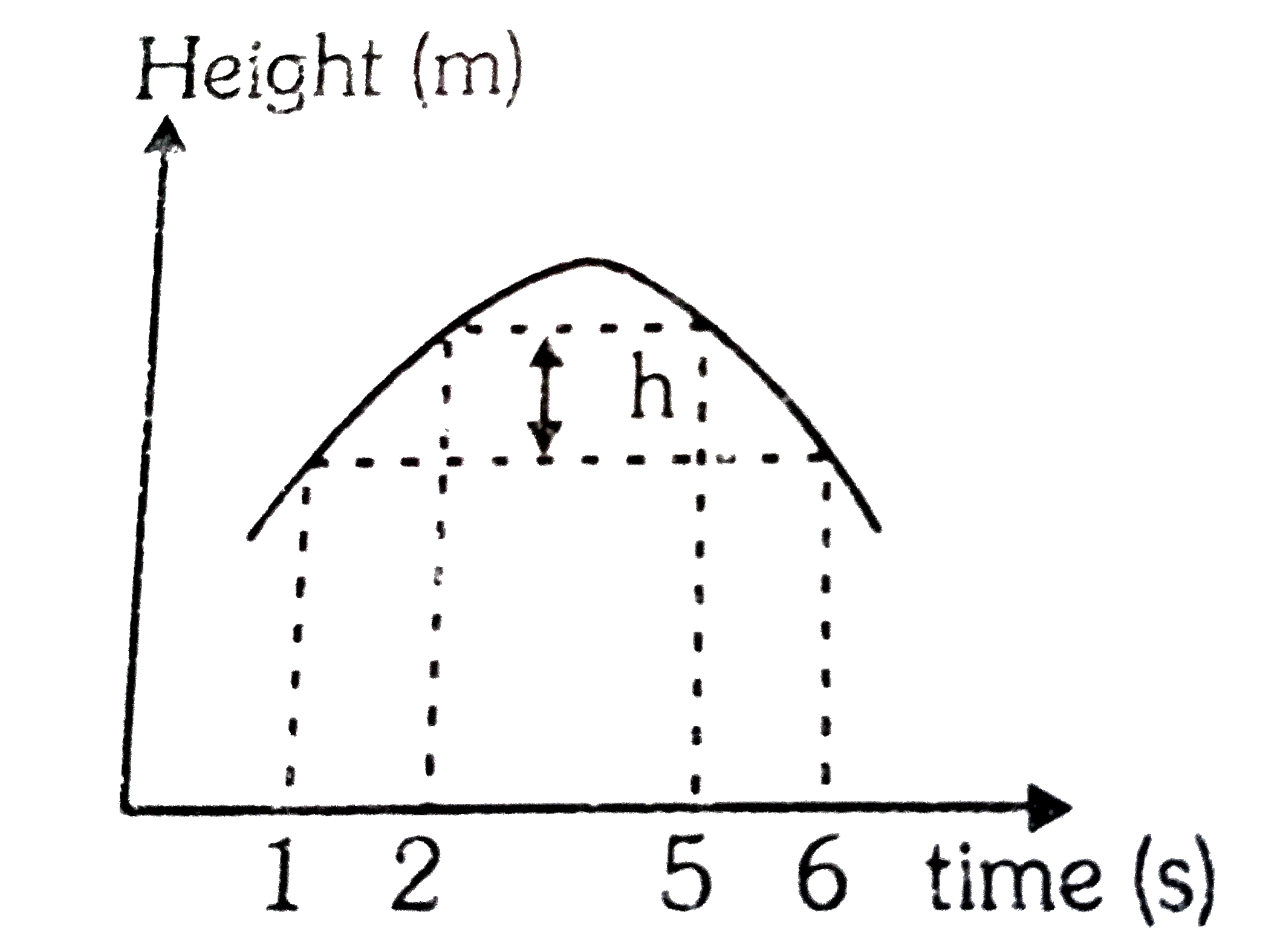
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View Solution
