In a frequency curve of scores, the mode was found to be higher than the mean. This shows that the distribution is Solution in Bengali
symmetric
negatively skewed
positively skewed
normal
Step by step video & image solution for In a frequency curve of scores, the mode was found to be higher than the mean. This shows that the distribution is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Proportion of girls in a class of 100 students is
View SolutionThe algebric sum of diviation of a set of n values from their arithmetic means is a
View Solutionनिम्न तालिका में 20 छात्रों के प्राप्तांकों का बारम्बारता वितरण दर्शाया गया है। इनका माध्य तथा मानक विचलन ज्ञात कीजिए -

View SolutionIf the mode and median of a frequency distribution are 31 and 37 respectively, find the arithmetic mean.
View SolutionIf the mean and median of a frequency distribution are 35 and 33 respectively, find mode.
View SolutionThe following distribution table shows the marks scored by 140 students in an examination :
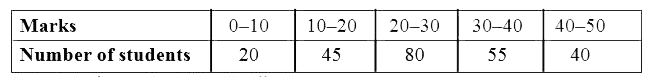
Calculate the mode of the distribution.
View SolutionIf in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately :
View SolutionIn a frequency distribution , the mean and median are 21 and 22 respectively , then its mode is approximately
View SolutionThe following distribution shows the marks scored by 140 students in an examination. Calculate the mode of the distribution :

View SolutionFind the mean and mode of the following frequency distribution :

View SolutionThe relation between mean, median, and mode for a frequency distribution is
View Solutionनिम्नलिखित सारणी किसी परीक्षा में 800 विद्यार्थियों के प्राप्तांकों के संचयी बारंबारता बंटन को दर्शाती है:
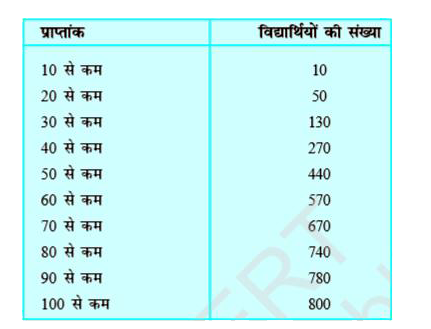
उपरोक्त आंकड़ों के लिए एक बारंबारता बंटन सारणी की रचना कीजिए।
View SolutionThe median and mode of a frequency distribution are 26 and 29 then its mean is
View SolutionIn a frequancy distribution,if the mean = 35 & median = 33, then find the mode of the frequency distribution.
View SolutionIf the median and mean of moderately asymmetrical frequency distribution are 72 and 74 respectively, then the mode is
View Solution

