तीन तरंगों के समीकरण y1=A0sin(kx−ωt),y2=3√2A0sin(kx−ωt+ϕ) औरy3=4A0cos(kx−ωt) द्वारा दिए गए हैं। ये तरंगें एक ही दिशा में गमन करती हैं और अध्यारोपित होती हैं। परिणामी-तरंग और पहली तरंग के बीच कलांतर π4 और ϕ=πn≤π2 है, तो n का मान क्या है?
The correct Answer is:12.00
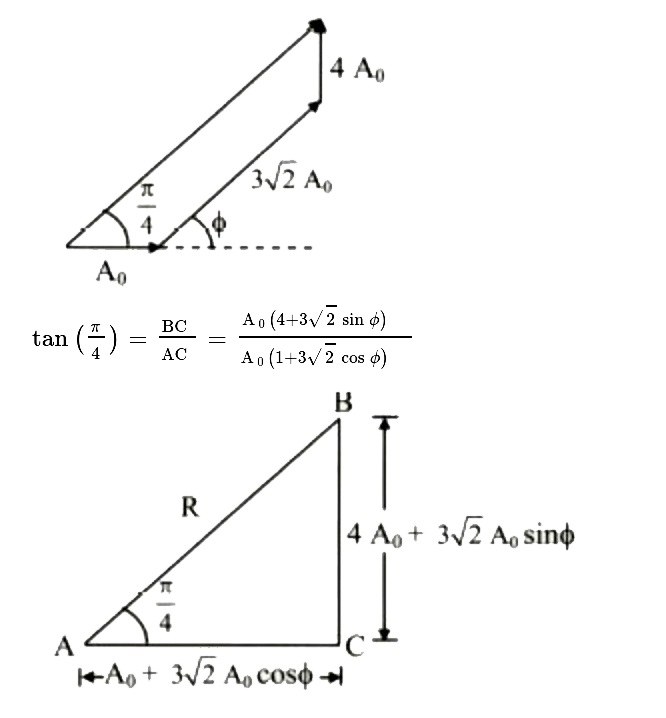
tan(π4)=BCAC=A0(4+3√2sinϕ)A0(1+3√2cosϕ)

⇒cosϕ−sinϕ=1√2
दोनों पक्षों का वर्ग करने पर,
⇒cos2ϕ+sin2ϕ−2cosϕsinϕ=12
⇒2sinϕcosϕ=12
⇒sin2ϕ=12
⇒ϕ=12sin−1(12)=π12
Topper's Solved these Questions
Similar Questions
हाइड्रोजन परमाणु में इलेक्ट्रॉन n1 से n2 अवस्था में संक्रमण करता है। यदि प्रारंभिक अवस्था में इलेक्ट्रॉन का आवर्त काल अंतिम अवस्था में आवर्त काल का आठ गुना है, तो n1 और n2 के संभावित मान क्या हैं?
View Solutionएक कण A से B 40 km/h चाल से एवं B से C 60 km/h चाल से गति करता है। यदि AB= 6BC.A एवं C के मध्य औसत चाल होगी।
View SolutionAssertion: Two equations of wave are y_(1)=A sin(omegat - kx) and y_(2) A sin(kx - omegat) . These two waves have a phase difference of pi . Reason: They are travelling in opposite directions.
View SolutionThree travelling waves are superimposed. The equations of the wave are y_(!)=A_(0) sin (kx-omegat), y_(2)=3 sqrt(2) A_(0) sin (kx-omegat+phi) and y_(3)=4 A_(0) cos (kx-omegat) find the value of phi ("given "0 le phi le pi//2) if the phase difference between the resultant wave and first wave is pi//4
View SolutionTwo sinusoidal waves are superposed. Their equations are
y1=Asin(kx−ωt+π6)andy2=Asin(kx−ωt−π6)
the equation of their resultant is
View Solutionचार प्रगामी तरंगों W1,W2,W3 एवं W4 के समीकरण हैं, क्रमश: y=A0sin(kx−ωt),y=A0sin(kx+ωt),y=A0cos(kx−ωt) तथा y=A0cos(kx+ωt0) । अप्रगामी तरंग बन सकती है
View SolutionTwo SHMs are respectively represented by y_(1)=a sin (omegat-kx) and y_(2)=b cos(omegat-kx) . The phase difference between the two is
View Solutionदो प्रकाश तरंगें y1=a1sinωt तथा y2=a2cos(ωt+ϕ) के मध्य पथान्तर कितना होगा?
View SolutionTwo waves y_(1) = a sin (omegat - kx) and y_(2) = a cos(omegat - kx) superimpose at a point :
View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"sec A का मान-1 और 1 के बीच में होता है
View SolutionThree travelling waves are superimposed. The equations of the wave are
y!=A0sin(kx−ωt),y2=3√2A0sin(kx−ωt+ϕ) and y3=4A0cos(kx−ωt)
find the value of ϕ(given 0≤ϕ≤π/2) if the phase difference between the resultant wave and first wave is π/4
View SolutionAssertion: Two equations of wave are y_(1)=A sin(omegat - kx) and y_(2) A sin(kx - omegat) . These two waves have a phase difference of pi . Reason: They are travelling in opposite directions.
View SolutionFollowed by a straight line. The three waves transmitted are as follows - 2A sin(kx - omegat + pi/3), sqrt(3)A cos(kx - omegat - pi/3) 2sqrt(3)A cos(kx - omegat + pi/3)
View SolutionTwo sinusoidal waves are superposed. Their equations are
y1=Asin(kx−ωt+π6)andy2=Asin(kx−ωt−π6)
the equation of their resultant is
View SolutionStatement! : Two wave equations are y_(1) = A sin(omegat -kx) and y_(2) =A sin(kx - omegat) . These two waves have a phase difference of pi . Statement-II : They are travelling in opposite directions.
View Solution
