अपचयित ताप =θ=tTc
अपचयित दाब −π=PPc
अपचयित आयतन =ϕ=vvc
अतः अवस्था का अपचयित समीकरण इस तरह हो सकता है
(π3+1ϕ2)(3ϕ−1)=83θ
(π3+1ϕ)(ϕ−1)=83θ
(π4+1ϕ)(3θ−1)=83ϕ
(π3+1ϕ)(3ϕ−1)=83ϕ
The correct Answer is:A
P=Pcπ=(a27b2)π
V=Vcϕ=(3b)ϕ
T=Tcθ=(8a27Rb)θ
इसलिए, वान्डरवाल समीकरण में प्रतिस्थापित करने पर,
P=Pcπ=(127b2)π
⇒(π+3ϕ2)(3ϕ−1)=8θ
यह अपचयित अवस्था समीकरण है।
(π+3ϕ2)(3ϕ8θ−18θ)=1
(π3+1ϕ2)(3ϕ−1)=83θ
Topper's Solved these Questions
- JEE- MAIN TEST 2BOOK - NTA MOCK TESTSCHAPTER - JEE- MAIN TEST 2EXERCISE - रसायन विज्ञान (विषयपरक आंकिक)
5 Videos
- JEE- MAIN TEST 1BOOK - NTA MOCK TESTSCHAPTER - JEE- MAIN TEST 1EXERCISE - रसायन विज्ञान (विषयपरक आंकिक)
5 Videos
- JEE- MAIN TEST 4BOOK - NTA MOCK TESTSCHAPTER - JEE- MAIN TEST 4EXERCISE - रसायन विज्ञान
25 Videos
Similar Questions
गर्म करने पर PCl5 वाष्प का वियोजन, निम्न अभिक्रिया के अनुसार होता है PCl5(g)⇔PCl3(g)+Cl2(g)
1.0 atm दाब और 500 K ताप पर आंशिक रूप से विघटित PCl5 के एक नमूने का घनत्व 4.8g/L पाया गया । 500 K ताप पर अभिक्रिया के लिए वियोजन की कोटि और ΔG∘ की गणना कीजिए।
(दिया गया है R=0.082LatmK−1mol−1,R=8.314JK−1mol_1,Inx=2.303log10x)
View Solutionआँकड़ों का उपयोग करते हुए KJmol−1 में फ्यूरेन की कणन की ऊष्मा की गणना करें
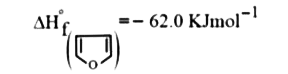
C, H, O के कणन की ऊष्मा 717, 218, 249 KJ mol−1 है। 100 से भाग देकर अपने उत्तर का चयन करें -
View Solutionएक एकलप्रोटिक अम्ल (d=1.01g/cm3) का 0.10 M विलयन 5 % आयनित होता है। विलयन का हिमांक बिंदु क्या है?अम्ल का अणु भार 300gmol और Kf(H2O)=1.86∘C/m है
View Solutionउन परिस्थतियों का अनुमान लगाइए जिनमें AI MgO को अपचयित कर सकता है।
View Solutionनिम्नलिखित में से कौन सा डाइसैकेराइड, टॉलेन अभिकर्मक को अपचयित नहीं करेगा ?
View Solutionकॉपर को अम्लीय कॉपर सल्फेट विलयन से किसके द्वारा अपचयित क्या जा सकता है ?
View Solution2-मेथिलपेंट-2-ईन अपचयित ओज़ोनी अपघटन पर क्या उत्पन्न करेगा?
View Solutionनिम्नलिखित में से कौन टॉलेन अभिकर्मक को अपचयित करेगा?
View Solutionअम्लीय माध्यम में नाइट्रोबेंजीन के 26.6 g को ऐनिलीन में अपचयित करने के लिए आवश्यक विद्युत् धारा है:
View Solutionनीचे दिए गए आरेख के अनुसार, A, BO_2 को अपचयित कर देता है जबकि तापमान होता है-
View Solutionनिम्नलिखित में से कौनसा कार्बनिक यौगिक टॉलेन अभिकर्मक को अपचयित कर सकता है?
View Solutionजब प्रोपिऑनिक अम्ल को हाइड्रोआयाडिक अम्ल और लाल फॉफोरस के साथ अपचयित किया जाता है तो निर्मित उत्पाद है
View Solutionदिए गए कौनसे यौगिक को संगत हाइड्रोकार्बन देने के लिए जिंक और हाइड्रोक्लोरिक अम्ल के साथ अपचयित किया जा सकता है?
View Solutionअपचयित ओजोनोपघटन पर एक ओलिफिनिक यौगिक फार्मेल्डिहाइड, एसीटैल्डिहाइड और 1 ,3 -प्रोपेनडाइ अल का निर्माण करता है। एल्कीन का IUPAC नाम है :
View Solutionनिम्नलिखित में से कौन टॉलेन अभिकर्मक को अपचयित नहीं करता है?
View Solution
