Let (x, y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0, 0) to (x, y) in the ratio 1 : 3. Then the locus of P is
x2=y
y2=2x
y2=x
x2=2y
The correct Answer is:C
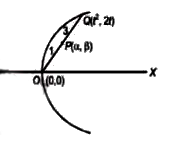
Let P(α,β) be the point intersecting the line-segment O(0,0) and Q(t2,2t) in the ratio 1:3.
Then α=t2+04,β=2t+04
⇒α=t24,β=t2
⇒4α=(2β)2
⇒β2=α
Locus of (α,β) is y2=x
Similar Questions
Let O be the vertex and Q be any point on the parabola,x2=8y . It the point P divides the line segment OQ internally in the ratio 1 : 3, then the locus of P is : (1) x2=y (2) y2=x (3) y2=2x (4) x2=2y
View SolutionThe point P(x,y) divide the line segment joining A(2,2) and B(3,4) in the ratio 1.2 then x+y is
View Solution
Knowledge Check
Let (x, y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0, 0) to (x, y) in the ratio 1:3. Then locus of P is
Ax2=yBy2=2xCy2=xDx2=2yLet (x,y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
Ax2=yBy2=2xCy2=xDx2=2yLet P be a point on x2=4y. The segment joining A(0,−1) and P is divided by point Q in the ratio 1:2, then locus of point Q is
A9x2=3y+2B9x2=12y+8C9y2=12x+8D9y2=3x+2
Let P be a point on the parabola y2−2y−4x+5=0, such that the tangent on the parabola at P intersects the directrix at point Q. Let R be the point that divides the line segment PQ externally in the ratio 12 : 1. Find the locus of R.
View SolutionLet (a,b) be a point on the parabola y=4x−x2 and is the point nearest to the point A(-1,4) Find (a+b).
View SolutionThe point P divides the join of (2,1) and (−3,6) in the ratio 2:3. Does P lie on the line x−5y+15=0?
View SolutionIf P is point on the parabola y2=8xandA is the point (1,0), then the locus of the mid point of the line segment AP is
View Solutionif the line 4x+3y+1=0 meets the parabola y2=8x then the mid point of the chord is
View Solution