A ray of light moving in air strikes at origin at grazing angle and then follows a path 2y=x2 for x≥0. The correct variation of refractive index with x co-ordinate is:
√1+4x2
√1+2x2
√1+x2
√1+x22
To solve the problem, we need to find the variation of the refractive index (μ) with respect to the x-coordinate for a ray of light that follows the path described by the equation 2y=x2 after striking the origin at a grazing angle.
1. Understand the Path of the Ray:
The path of the ray is given by the equation 2y=x2, which can be rewritten as:
y=x22
This represents a parabolic curve opening upwards.
2. Find the Slope of the Tangent:
To find the angle of incidence, we need to determine the slope of the tangent to the curve at any point. We can find this by differentiating y with respect to x:
dydx=ddx(x22)=x
The slope of the tangent line at any point on the curve is x.
3. Determine the Angle of Incidence:
The angle of incidence (θ) can be determined using the tangent of the angle:
tanθ=dydx=x
Therefore, we can express θ in terms of x:
θ=tan−1(x)
4. Apply Snell's Law:
According to Snell's law, when light travels from one medium to another, we have:
n1sini=n2sinr
Here, n1=1 (the refractive index of air), i=90∘ (grazing angle), and r=90∘−θ. Thus, we can write:
1⋅sin(90∘)=μ⋅sin(90∘−θ)
This simplifies to:
1=μ⋅cosθ
5. Relate Cosine to x:
We know that:
cosθ=1√1+tan2θ=1√1+x2
Therefore, substituting this into our equation gives:
1=μ⋅1√1+x2
6. Solve for the Refractive Index (μ):
Rearranging the equation to solve for μ:
μ=√1+x2
Final Result:
The variation of the refractive index with respect to the x-coordinate is given by:
μ=√1+x2
The path of the ray is given by the equation 2y=x2, which can be rewritten as:
y=x22
This represents a parabolic curve opening upwards.
To find the angle of incidence, we need to determine the slope of the tangent to the curve at any point. We can find this by differentiating y with respect to x:
dydx=ddx(x22)=x
The slope of the tangent line at any point on the curve is x.
The angle of incidence (θ) can be determined using the tangent of the angle:
tanθ=dydx=x
Therefore, we can express θ in terms of x:
θ=tan−1(x)
According to Snell's law, when light travels from one medium to another, we have:
n1sini=n2sinr
Here, n1=1 (the refractive index of air), i=90∘ (grazing angle), and r=90∘−θ. Thus, we can write:
1⋅sin(90∘)=μ⋅sin(90∘−θ)
This simplifies to:
1=μ⋅cosθ
We know that:
cosθ=1√1+tan2θ=1√1+x2
Therefore, substituting this into our equation gives:
1=μ⋅1√1+x2
Rearranging the equation to solve for μ:
μ=√1+x2
The variation of the refractive index with respect to the x-coordinate is given by:
μ=√1+x2
Topper's Solved these Questions
Similar Questions
If a ray of light propagating in air strikes a glass slab at an angle of 30∘ with the surface of the slab, the angle of refraction is
View SolutionA ray of light travelling in air is incident at grazing angle (incidence angle =90∘) on a medium whose refractive index depends on the depth of the medium. The trajectory of the light in the medium is a parabola, y=2x2. Find, at a depth of 1 m in the medium
(i) the refractive index of the medium and
(ii) angle of incidence ϕ.
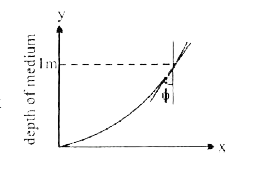
View Solution
Knowledge Check
If a ray of light propagating in air strikes a glass slab at an angle of 60∘ with the surface of the slab, the angle of refraction is …......................
Amore than 30∘Bless than 30∘C60∘D30∘A ray of light strikes a material's slab at an angle of incidence 60∘. If the reflected and refracted rays are perpendicular to each other, the refractive index of the material is
A1√3B1√2C√2D√3A ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
A(a) 90∘+ϕB(b) sin−1(μcosϕ)C(c) 90∘D(d) 90∘−sin−1(sinϕ/μ)
A ray of light travelling in air is incident at grazing angle (incident angle = 90∘) on a large rectangular slab of a transparent medium of thickness t = 1 m. The point of incidence js the origin A (0, 0). The medium has a refractive index of n (y) given
n(y)=(9ky32+1)12
Where K = (meter)−32, The refractive index of air is 1.
Obtain the equation for the trajectory y(x) of the ray of the medium.
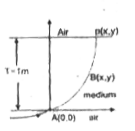
View SolutionA ray of light travelling in air is inciden at angle of inciden 30∘ on one surface of slab in which refractive index varies with y. The light travels along the curve y=4x2 ( y and x are in meter) in the slab. Find out the refractive index of the slab at y=1/2m in the slab.

View SolutionA ray of light strikes a glass plate at an angle of incidence 57∘ . If the reflected and refracted rays are perpendicular to each other, what is the refractive index of glass.
View SolutionA ray of light, travelling in a medium of refractive index mu, is incident at an angle i on a composite transparent plate consisting of three plates of refractive indices μ1,μ2andμ3. The ray emerges from the composite plate into a medium of refractive index μ4, at angle x. Then,
View SolutionA ray of light strikes a glass plate at an angle of 40∘. If the reflected and refracted rays are perpendicular to each other the index of refractive of glass is
View Solution