Let σ1,σ2,σ3 be planes passing through the origin. Assume that σ1 is perpendicular to the vector (1,1,1), σ2 is perpendicular to a vector (a,b,c) and σ3 is perpendicular to the vector (a2,b2,c2). What are all the positive values of a,b and c so that σ1∩σ2∩σ3 is a single point?
Any positive value of a,b, and c other than 1
Any positive values of a,b and c where either a≠b,b≠c or a≠c
Any three distinct positive values of a,b and c
There exist no such positive real numbers a,b,and c
To solve the problem, we need to find the conditions under which the intersection of three planes, σ1, σ2, and σ3, is a single point. Let's go through the solution step by step.
Step 1: Write the equations of the planes
1. Plane σ1 is perpendicular to the vector (1,1,1). Therefore, its equation can be written as:
x+y+z=0
2. Plane σ2 is perpendicular to the vector (a,b,c). Thus, its equation is:
ax+by+cz=0
3. Plane σ3 is perpendicular to the vector (a2,b2,c2). Hence, its equation is:
a2x+b2y+c2z=0
Step 2: Set up the determinant
To find the intersection of these three planes, we can set up a determinant using the coefficients of x, y, and z from the equations of the planes:
∣∣
∣∣111abca2b2c2∣∣
∣∣
Step 3: Calculate the determinant
We will calculate the determinant:
D=∣∣
∣∣111abca2b2c2∣∣
∣∣
Using the determinant formula, we can expand it:
D=1⋅(b⋅c2−c⋅b2)−1⋅(a⋅c2−c⋅a2)+1⋅(a⋅b2−b⋅a2)
This simplifies to:
D=bc2−b2c−ac2+a2c+ab2−a2b
Step 4: Factor the determinant
We can factor the determinant:
D=(a−b)(b−c)(c−a)
Step 5: Condition for a unique intersection point
For the intersection of the three planes to be a single point, the determinant must not be zero:
(a−b)(b−c)(c−a)≠0
This means that a, b, and c must be distinct values.
Conclusion
Thus, the positive values of a, b, and c such that the intersection of the three planes σ1, σ2, and σ3 is a single point are any three distinct positive values.
1. Plane σ1 is perpendicular to the vector (1,1,1). Therefore, its equation can be written as:
x+y+z=0
ax+by+cz=0
a2x+b2y+c2z=0
To find the intersection of these three planes, we can set up a determinant using the coefficients of x, y, and z from the equations of the planes:
∣∣
∣∣111abca2b2c2∣∣
∣∣
We will calculate the determinant:
D=∣∣
∣∣111abca2b2c2∣∣
∣∣
D=1⋅(b⋅c2−c⋅b2)−1⋅(a⋅c2−c⋅a2)+1⋅(a⋅b2−b⋅a2)
This simplifies to:
D=bc2−b2c−ac2+a2c+ab2−a2b
We can factor the determinant:
D=(a−b)(b−c)(c−a)
For the intersection of the three planes to be a single point, the determinant must not be zero:
(a−b)(b−c)(c−a)≠0
This means that a, b, and c must be distinct values.
Thus, the positive values of a, b, and c such that the intersection of the three planes σ1, σ2, and σ3 is a single point are any three distinct positive values.
Topper's Solved these Questions
Similar Questions
The position vectors of the points A,B,C are respectively (1,1,1),(1,-1,2),(0,2,-1). Find a unit vector parallel totehplane determined by A,B,C and perpendicular to the vector (1,0,1).
View SolutionThe figure shows three infinite non-conducting plates of charge perpendicular to the plane of the paper with charge per unit area +σ,+2σ and −σ. Find the ratio of the net electric field at that point a to that at point B.
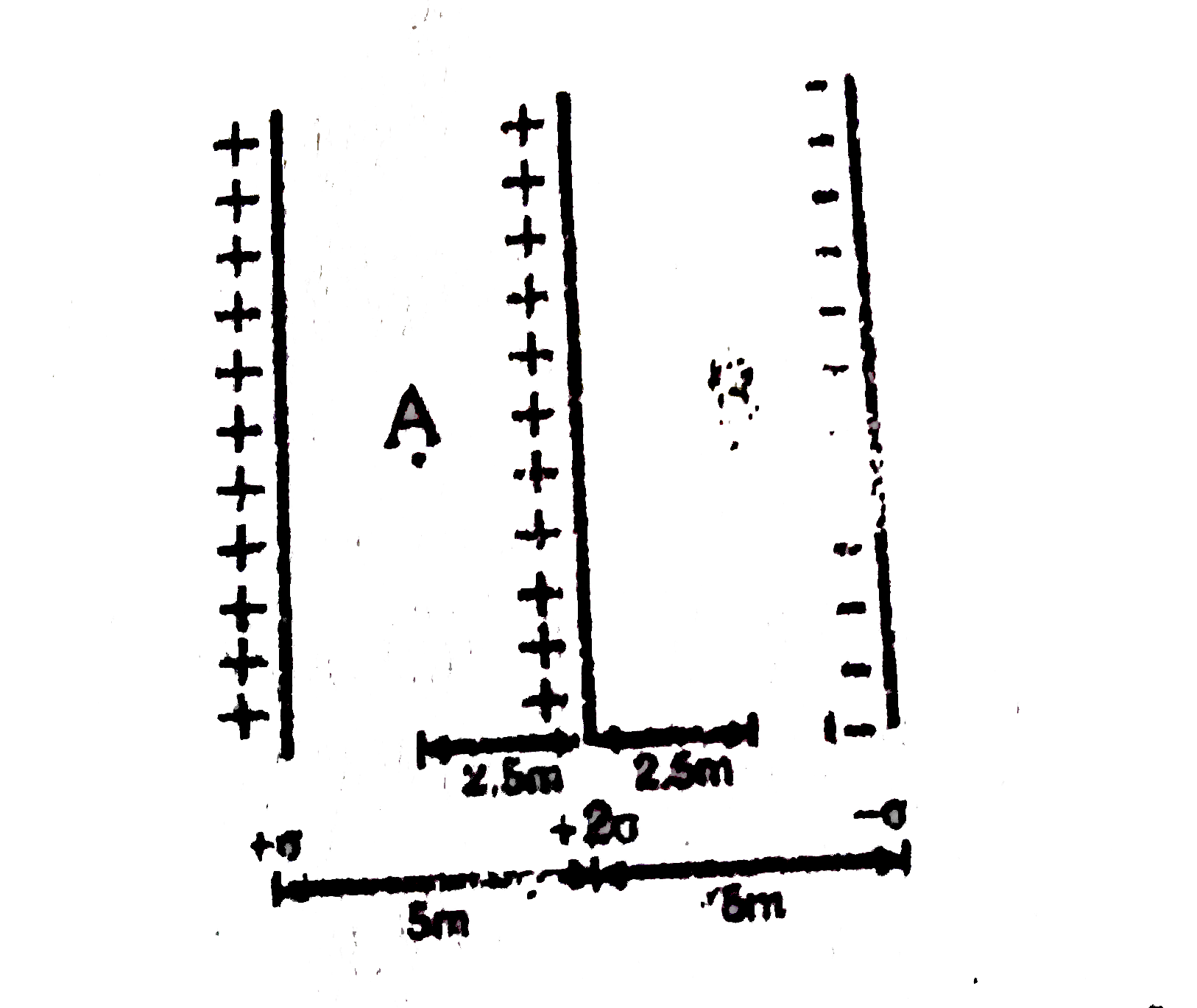
View Solution
Knowledge Check
If X is a random variable such that σ(X)=2.6, then σ(1−4X) is equal to
A7.8B−10.4C13D10.4Two spheres of radii 2 cm and 3 cm are charged to the same potential. If σ and σ2 be respectively the values of surface charge density on the conductors, then the ratio σ1σ2 will be
A49B23C32D94Two spherical conductors of radii 4 m and 5 m are charged to the same potential. If σ1andσ2 be the respective value of the surface density of charge on the two conductors, then the ratio σ1σ2is
A2516B1625C54D45
Let X be a random variable with distribution.
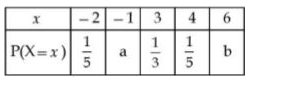
If the mean of X is 2.3 and variance of X is σ2, then 100σ2 is equal to :
View SolutionLet X be a random variable with distribution.
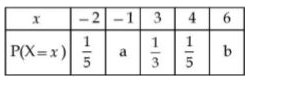
If the mean of X is 2.3 and variance of X is σ2, then 100σ2 is equal to :
View SolutionThe energy of σ2x, is greater than that of σ∗1s orbital because
View SolutionTwo spherical conductors of radii 4cmand5cm are charged to the same potential. If σ1andσ2 be respective value of surface density of charge on both the conductors, then the ratio of σ1/σ2 will be
View SolutionElectrical conductivies of Ge and Na are σ1 and σ2 respectively. If these substances are heard, then
View Solution
