For a uniformly charged non conducting sphere of radius R which of following shows a correct graph between the electric field intensity and the distance from the centre of sphere –
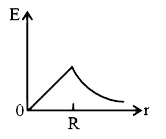

The correct Answer is:A
To solve the question regarding the electric field intensity (E) around a uniformly charged non-conducting sphere of radius R, we need to analyze the behavior of the electric field both inside and outside the sphere.
1. Understanding the Problem: We have a uniformly charged non-conducting sphere with radius R. We need to determine how the electric field intensity varies with distance from the center of the sphere.
2. Electric Field Inside the Sphere:
- For a point inside the uniformly charged non-conducting sphere (where distance r<R), the electric field intensity E can be calculated using Gauss's Law.
- The formula for the electric field inside the sphere is given by:
E=14πϵ0⋅Q⋅rR3
where Q is the total charge of the sphere, r is the distance from the center, and R is the radius of the sphere.
- This shows that the electric field inside the sphere is directly proportional to the distance r from the center.
3. Electric Field Outside the Sphere:
- For a point outside the uniformly charged non-conducting sphere (where distance r≥R), the electric field behaves as if all the charge were concentrated at the center of the sphere.
- The formula for the electric field outside the sphere is:
E=14πϵ0⋅Qr2
- This indicates that the electric field outside the sphere is inversely proportional to the square of the distance r.
4. Graphical Representation:
- Inside the sphere (for r<R), the electric field increases linearly with distance from the center.
- At the surface of the sphere (at r=R), the electric field reaches a maximum value.
- Outside the sphere (for r>R), the electric field decreases with the square of the distance.
5. Conclusion:
- The correct graph would show a linear increase in electric field intensity from the center to the surface of the sphere and then a decrease as we move further away from the sphere.
- For a point inside the uniformly charged non-conducting sphere (where distance r<R), the electric field intensity E can be calculated using Gauss's Law.
- The formula for the electric field inside the sphere is given by:
E=14πϵ0⋅Q⋅rR3
where Q is the total charge of the sphere, r is the distance from the center, and R is the radius of the sphere.
- This shows that the electric field inside the sphere is directly proportional to the distance r from the center.
- For a point outside the uniformly charged non-conducting sphere (where distance r≥R), the electric field behaves as if all the charge were concentrated at the center of the sphere.
- The formula for the electric field outside the sphere is:
E=14πϵ0⋅Qr2
- This indicates that the electric field outside the sphere is inversely proportional to the square of the distance r.
- Inside the sphere (for r<R), the electric field increases linearly with distance from the center.
- At the surface of the sphere (at r=R), the electric field reaches a maximum value.
- Outside the sphere (for r>R), the electric field decreases with the square of the distance.
- The correct graph would show a linear increase in electric field intensity from the center to the surface of the sphere and then a decrease as we move further away from the sphere.
Similar Questions
The electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionAn isolated non-conducting solid sphere of radius R is given an electric charge. The charge is uniformly distributed in the volume of sphere. The graph which shows the correct variation of magnitude of electric field with distance from the centre of the sphere is
View Solution
Knowledge Check
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
ARVr2BVRCrVR2DR2Vr2A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
AVrBR2Vr3CRVr2DrVR2Figure shows two concentric shells of radii a and b uniformly distributed charges q and -q. Which of the following graphs gives correct variation of electric field intensity E with the distance r from the centre?
 A
A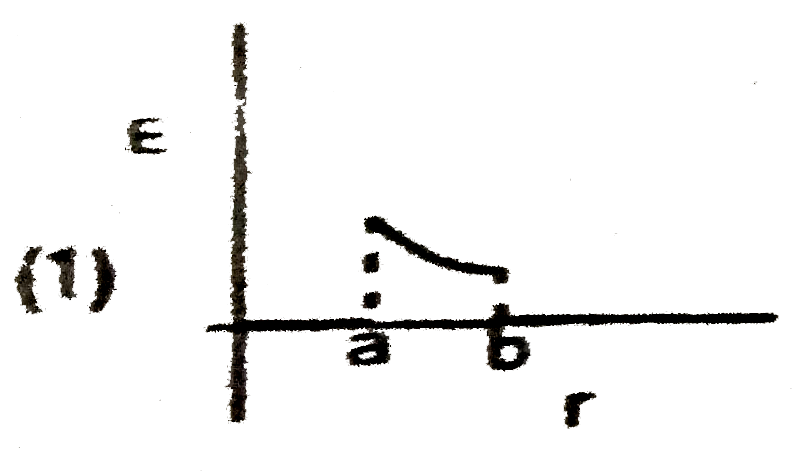 B
B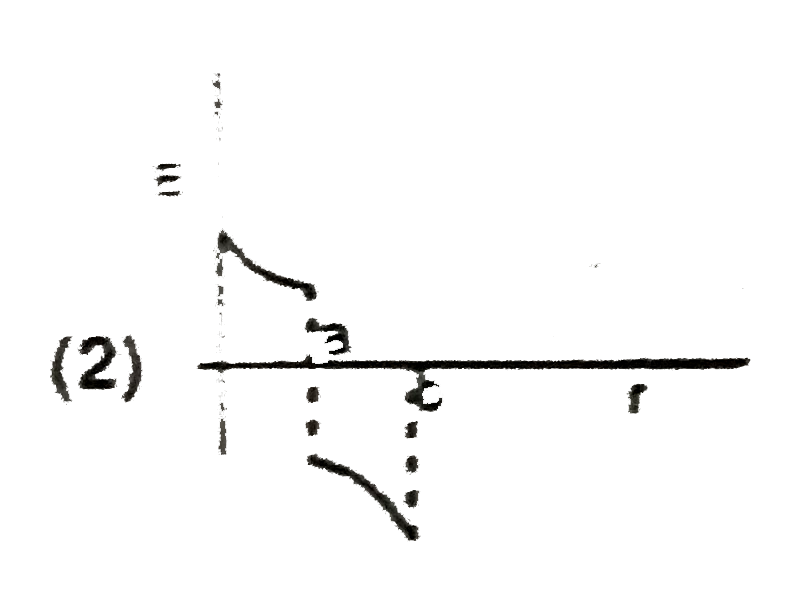 C
C D
D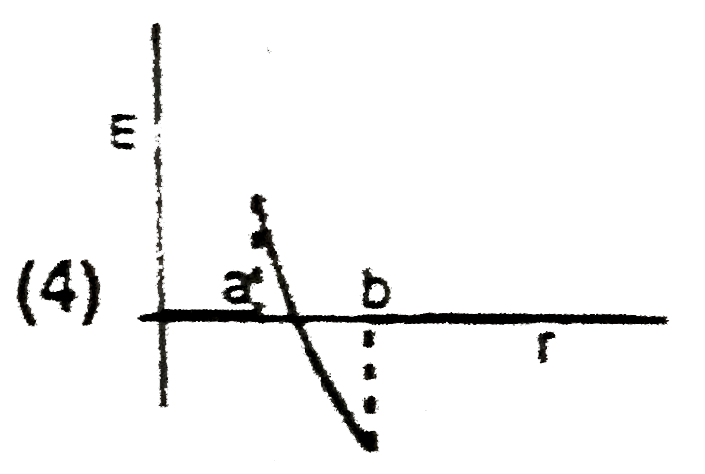
A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA sphere of radius R, is charged uniformly with total charge Q. Then correct statement for electric field is (r = distance from centre): -
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View SolutionAt a point 20cm from the centre of a uniformly charged dielectric sphere of radius 10cm, the electric field is 100V/m. The electric field at 3cm from the centre of the sphere will be
View Solution
