Derive the expression for the electric potential at any point along the axial line of an electric dipole.
Electric potential due to a dipole at a point on the end-on position: Figure below shows a dipole consisting of two equal and opposite charges +q and -q separated by a distance 2l. Let P be a point on the end-on position (on the axis) of the dipole. OP is the axial line of the dipole.
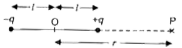
The potential due to the charge +q at the point P=V1
V1=14πε0qr−1
The potential due to the charge -q at the point P=V2
V2=14πε0.(−q)(r+l)
Total potential at the point P V=V1+V2
=14πε0qr−l+14πε0(−q)(r+l)
=q4πε0[1r−l−1r+l]
=q4πε0[r+l−r+l(r−l)(r+l)]
=14πε0.2lqr2−l2
But the dipole moment p= 2lq
So, V=14πε0.p(r2−l2)
Suppose r>>l. Then l2 can be neglected compared to r2. So for a short dipole, the electric potential at a point on the end-on position is,
V=14πε0.pr2
Similar Questions
(a) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
(b) Derive an expression for the electric potential at any point along the axial line of an electric dipole
View SolutionAnswer the following:
(a) Derive and expression for the electric field at any point on the equatorial line of an electric dipole.
(b) Two identical point charges, q each kept 2m apart in air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
View Solution(i) Derive the expression for electric field at a point on the equatorial line of an electric dipole.
(ii) Depiet the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
View Solution(a) Define electric dipole moment. Is it a scalar or a vector ? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
View SolutionAnswer the following:
(a) Derive the expression for the electric potential at any point P, at distance r from the centre of an electric dipole, making angle α, with its axis.
(b) Two point charges 4μCand+1μC are separated by a distance of 2m in air. Find the point on the line joining charges at which the net electric field of the system is zero.
View SolutionWhat will be electric potential at any point on the perpendicular bisector of an electric dipole?
View SolutionElectric potential at any point in equatorial plane of a dipole is ………. .
View SolutionThe value of electric potential at any point due to any electric dipole is
View SolutionObtain an expression for intensity of electric field in end on position, i.e., axial position of an electric dipole.
View Solution(i) Derive the expression for the specific for the electric potential due to an electric dipole at a point on its axial line.
(ii) Depiet the equivpotential surfaces due to an electric dipole.
View Solution