What is the value of power factor for a pure resistor connected to an alternating current source?
To find the value of the power factor for a pure resistor connected to an alternating current (AC) source, we can follow these steps:
1. Understanding Power Factor:
The power factor (PF) is defined as the cosine of the phase angle (φ) between the voltage and current in an AC circuit. It is given by the formula:
Power Factor=cosϕ
2. Identifying Circuit Components:
In this case, we have a pure resistor connected to an AC source. This means there are no inductors or capacitors in the circuit.
3. Impedance in the Circuit:
The impedance (Z) in an AC circuit is given by:
Z=√R2+(XL−XC)2
where R is the resistance, XL is the inductive reactance, and XC is the capacitive reactance. Since we have a pure resistor, XL=0 and XC=0.
4. Calculating Impedance:
With XL and XC being zero, the impedance simplifies to:
Z=√R2+0=R
5. Finding the Power Factor:
Now, we can find the power factor using the relationship:
cosϕ=RZ
Substituting Z=R:
cosϕ=RR=1
6. Conclusion:
Therefore, the value of the power factor for a pure resistor connected to an AC source is:
Power Factor=1
Final Answer:
The value of the power factor for a pure resistor connected to an alternating current source is 1.
The power factor (PF) is defined as the cosine of the phase angle (φ) between the voltage and current in an AC circuit. It is given by the formula:
Power Factor=cosϕ
In this case, we have a pure resistor connected to an AC source. This means there are no inductors or capacitors in the circuit.
The impedance (Z) in an AC circuit is given by:
Z=√R2+(XL−XC)2
where R is the resistance, XL is the inductive reactance, and XC is the capacitive reactance. Since we have a pure resistor, XL=0 and XC=0.
With XL and XC being zero, the impedance simplifies to:
Z=√R2+0=R
Now, we can find the power factor using the relationship:
cosϕ=RZ
Substituting Z=R:
cosϕ=RR=1
Therefore, the value of the power factor for a pure resistor connected to an AC source is:
Power Factor=1
The value of the power factor for a pure resistor connected to an alternating current source is 1.
Similar Questions
What is the value of power factor for series LR circuit ?
View SolutionA bulb is designed to operate at 12 volts constant direct current.If this bulb is connected to an alternating current source and gives same brightness.What would be the peak voltage of the source?
View SolutionA bulb is designed to operate at 12 volts constant direct current.If this bulb is connected to an alternating current source and gives same brightness.What would be the peak voltage of the source?
View SolutionThe coefficient of induction of a choke coil is 0.1H and resistance is 12Ω. If it is connected to an alternating current source of frequency 60Hz, then power factor will be
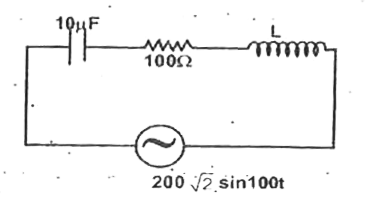
View SolutionA 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
View SolutionThe average power dissipated in a pure inductor L carrying an alternating current of rms value I is .
View SolutionThree equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
View SolutionThree equal resistors connected in series across a source of e.m.f. together dissipate 10 W of power. What should be the power dissipated if the same resistors are connected in parallel across the same source of e.m.f.
View SolutionIn the circuit shown there is a box and capacitance C connected to alternating power source of angular frequency of 2 rad//s. Box has power factor 1/√2 and circuit has overall power factor 1
1. Find the impedance of the box
View SolutionA resistor R1 consumes electrical power P1 when connected to an emfε. When resistor R2 is connected to the same emf , it consumes electrical power P2 . In terms of P1andP2, what is the total electrical power consumed when they are both connected to this emf source
(a) in parallel
(b) in series
View Solution
