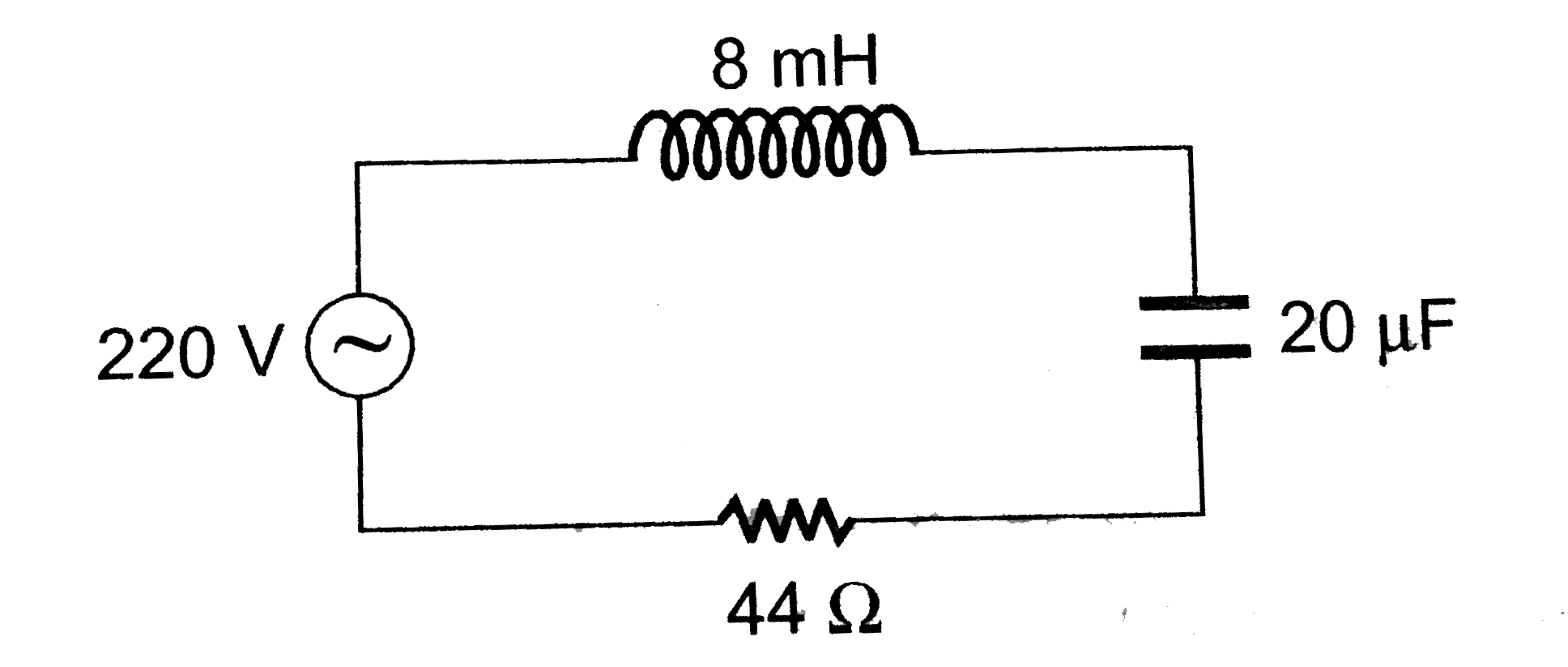In a series LCR circuit, obtain an expression for the resonant frequency.
Resonant frequency of LCR circuit : The current amplitude Io for a series LCR circuit is given by
I0=E0√R2+(ωL−1ωC)2
Clearly, I0 becomes zero both for ω→0andω→∞ . The value of I0 is maximum when
ωL−1ωC=0
LCR series circuit is said to be in resonance when inductive reactance is equal to capacitive reactance i.e., ωL=1ωC
or ω=1√LC
Then, impedance, Z=√R2+(ωL−1ωC)2
Clearly, the impedance is minimum. The circuit is purely resistive. The current and voltage are in the same phase and the current in the circuit is maximum. This condition of the LCR circuit is called resonance condition. The frequency at which the current ampitude I0 attains a peak value is called natural or resonant frequency of the LCR circuit and is denoted by fr .
Thus , ωr=2πfr=1√LC
or fr=12π√LC
Similar Questions
Knowledge Check
In a series LCR circuit having L=30mH,R=8Ω and the resonant frequency is 50 Hz. The quality factor of the circuit is
A0.118B11.8C118D1.18In the series LCR circuit shown the impedance is
 A200ΩB100ΩC300ΩD500Ω
A200ΩB100ΩC300ΩD500Ω
For the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency

View SolutionIn a series L-C-R circuit shown in the figure , what is the resonance frequency and the current at the resonating frequency?
View SolutionIn a series LCR circuit resonance of frequency is the half of the frequency of source.The nature of the circuit is
View SolutionPhase relationship between current (l) and applied voltage (E) for a series LCR circuit is shown here. ω0 = Resonant angular frequency of the circuit and ω= Applied angular frequency .
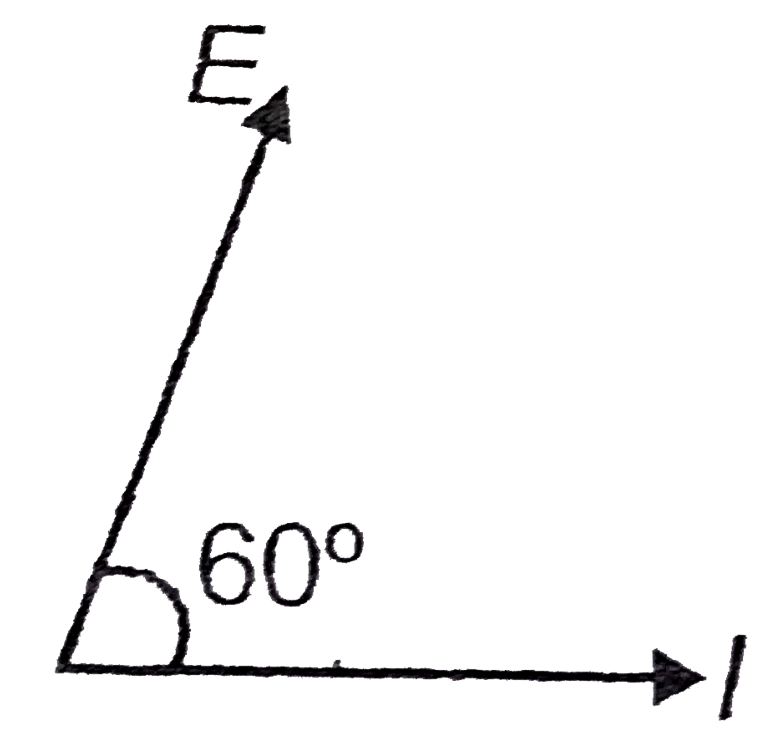
View SolutionIn the series LCR circuit shown the impedance is

View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View Solution