Show that electric potential at a point P, at a distance .r. from a fixed point charge Q, is given by :
V=(14πε0)Qr
Electric potential due to a point charge :
Consider a positive point charge Q placed at the origin O. We have to calculate its electric potential at a point P at a distance of r from it as shown in the figure. The electric potential at point P will be equal to the amount of work done in bringing a unit positive charge from infinity to point P.
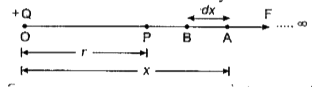
Suppose a test charge q0 is placed at a point A at a distance of x from O. By Coulomb.s law, the electrostatic force acting on charge g0 is,
F=14πε0.Qq0x2
The small work done in moving the test charge q0 from A to B through small displacement −→dx against the electrostatic force is
dW=→F.−→dx=Fdxcos180∘=−Fdx
The total work done in moving the charge go from infinity to the point P is given by
W=∫dW=−∫r∞Fdx
=−∫r∞14πε0−Qq0x2dx
=−Qq04πε0∫r∞x−2dx
W=−Qq04πε0[−1x]r∞
=Qq04πε0[1r−1∞]
=14πε0.Qq0r
The electric potential at P is the work done per unit charge from infinity to the point P.
V=Wq0
or V=14πε0.Qr
Similar Questions
A ring of radius R is having two charges q and 2q distributed on its two half parts. The electric potentiasl at a point on its axis at a distance of 2√2R from its centre is (k=14πε0)
View SolutionAlong the x-axis, three charges q2,−q and q2 are placed at x=0,x=a and x=2a respectively. The resultant electric potential at a point P located at a distance r from the charge −q, (r>>a) is : ( ε0 is the permittivity of free space)
View SolutionShow that intensity of electric field E at a point in broadside on position is given by :
E=(14πε0)p(r2+l2)3/2
where the terms have their usual meaning.
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View Solution
The figure shows two identical long straight metal wires, A and B placed parallel to z-axis the cross sectional radius of each wire is R and the separation of the two wires is D>>R. The electric potential at a perpendicular distance r>R from a long straight wire due to that wire is given by V=−kln(rR) where k is a positive constant. the wires carry charges +Q and −Q per unit length respectively. Then
Q. Consider a point P on the x-axis. The electric field at P is given by:
View SolutionSTATEMENT-1: For practical purposes, the earth is used as a reference at zero potencial in electrical circuits. and
STATEMENT-2: The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by Q4πε0R.
View SolutionElectric potential is a scalar quantity. Due to a point charge charge q at distance r, the potential is given by V=q4π∈0r. A point charge q is placed at (3a,0) and another charge −2q is placed at (−3a,0).
At how many points on the x-axis, (at finite distance) electric potential will be zero?
View SolutionFor spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View SolutionElectric potential is a scalar quantity. Due to a point charge charge q at distance r, the potential is given by V=q4π∈0r. A point charge q is placed at (3a,0) and another charge −2q is placed at (−3a,0).
If we plot a graph of potential (V) on x-axis it will be like:
View SolutionObtain an expression for electric potential .V due to a point charge .Q at a distance r.
View Solution