Find the angle of incidence at which a ray of monochromatic light should be incident on the first surface AB of a regular glass prism ABC so that the emergent ray grazes the adjacent surface AC.(Refractive Index of glass = 1.56)
To find the angle of incidence at which a ray of monochromatic light should be incident on the first surface AB of a regular glass prism ABC so that the emergent ray grazes the adjacent surface AC, we can follow these steps:
Step 1: Understand the Geometry of the Prism
The prism ABC is a regular glass prism, which means it has equal angles. For a regular prism, the angle of the prism (A) is 60 degrees.
Step 2: Define the Angles
Let:
- I = angle of incidence at surface AB
- R1 = angle of refraction at surface AB
- R2 = angle of refraction at surface AC
- The emergent ray grazes surface AC, meaning R2=90∘.
Step 3: Apply Snell's Law at Surface AB
Using Snell's Law at the first surface (AB):
μ1sinI=μ2sinR1
Where:
- μ1=1 (refractive index of air)
- μ2=1.56 (refractive index of glass)
This gives us:
sinI=1.56sinR1
Step 4: Apply Snell's Law at Surface AC
At the second surface (AC), since the emergent ray grazes the surface, we have:
μ2sinR2=μ1sinE
Where E=90∘, so:
sinR2=1
Thus, we have:
1.56sin90∘=1sinR2
This simplifies to:
sinR2=11.56
Step 5: Calculate R2
Calculating R2:
R2=arcsin(11.56)≈39.86∘ (approximately 40 degrees)
Step 6: Relate the Angles in the Prism
For a prism, the sum of the angles is given by:
A=R1+R2
Substituting the known values:
60∘=R1+40∘
Thus:
R1=60∘−40∘=20∘
Step 7: Substitute R1 into Snell's Law
Now substituting R1 back into Snell's Law:
sinI=1.56sin20∘
Calculating sin20∘:
sin20∘≈0.342
Thus:
sinI=1.56×0.342≈0.5335
Step 8: Calculate the Angle of Incidence I
Finally, we find I:
I=arcsin(0.5335)≈32.24∘
Final Answer
The angle of incidence at which the ray should be incident on surface AB is approximately 32.24∘.
---
The prism ABC is a regular glass prism, which means it has equal angles. For a regular prism, the angle of the prism (A) is 60 degrees.
Let:
- I = angle of incidence at surface AB
- R1 = angle of refraction at surface AB
- R2 = angle of refraction at surface AC
- The emergent ray grazes surface AC, meaning R2=90∘.
Using Snell's Law at the first surface (AB):
μ1sinI=μ2sinR1
Where:
- μ1=1 (refractive index of air)
- μ2=1.56 (refractive index of glass)
sinI=1.56sinR1
At the second surface (AC), since the emergent ray grazes the surface, we have:
μ2sinR2=μ1sinE
Where E=90∘, so:
sinR2=1
Thus, we have:
1.56sin90∘=1sinR2
This simplifies to:
sinR2=11.56
Calculating R2:
R2=arcsin(11.56)≈39.86∘ (approximately 40 degrees)
For a prism, the sum of the angles is given by:
A=R1+R2
Substituting the known values:
60∘=R1+40∘
Thus:
R1=60∘−40∘=20∘
Now substituting R1 back into Snell's Law:
sinI=1.56sin20∘
Calculating sin20∘:
sin20∘≈0.342
Thus:
sinI=1.56×0.342≈0.5335
Finally, we find I:
I=arcsin(0.5335)≈32.24∘
The angle of incidence at which the ray should be incident on surface AB is approximately 32.24∘.
Similar Questions
At what angle, a ray of light should be incident on the first face AB of a regular glass prism ABC so that the emergent ray grazes the adjacent face AC ?

View Solution(a) Deduce the expression, by drawing a suitable ray diagram, for the refractive index of a triangular glass prisms in terms of the angle of minimum deviation (D) and the angle of prism (A).
Draw a plot showing the variation of the angle of deviation with the angle of incidence.
(b) Calculate the value of the angle of incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of prism is √2
View Solution
Knowledge Check
A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
A1.732B1.414C1.5D1.33
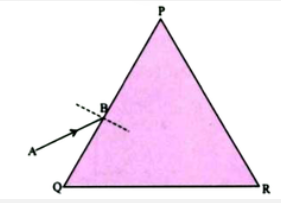
Complete the path of the monochromatic light ray AB incident on the surface PQ of the equilateral glass prism PQR till it emerges out of the prism due to refraction.
View SolutionThe angle at which a ray of light be incident on one face of an equilateral prism,so that the emergent ray may graze the second surface of the prism is πx rad.then find "x" .(μ=2)]
View SolutionA ray LM of monochromatic light incident normally on one refracting surface AB of a regular glass prism ABC emerges in air from the adjacent surface C as shown in figure. Calculate the refractive index of the material of the prism.
View SolutionA ray EF of monochromatic light is incident on the refracting surface AB of a regular glass prism ( refractive index=1.5) at angle of incidence i=55∘ (Figure). If it emerges the adjacent face AC, calculate the angle of emergence .e..
View SolutionA ray of light incident on the horizontal surface of a glass slab at 70∘ just grazes the adjacent vertical surface after refraction. Complete the critical angle and refractive index of glass.
View SolutionA ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View Solution

