Derive an expression for intensity of electric field are a point in broadside position or on an equatorial line of an electric dipole.
Suppose that the point P is situated on the right bisector of the dipole AB at a distance r metre from its mid-point [Fig. (a)].
Let E1andE2 be the magnitudes of the intensities of the electric field at P due to the charges + q and - 2 of the dipole respectively. The distance of P from each charge is √r2+l2. Therefore,
E1=14πε0q(r2+l2) away from +q
and E2=14πε0q(r2+l2). towards -q
The magnitudes of E1andE2 are equal t(but direction are different). On resolving E1andE2 into two components perpendicular to AB (E1sinθandE2sinθ) cancel other (beucse they are equal and opposite), while the components par4allel to AB (E1cosθE2cosθ). being in the same direction, add up [Fig.(b)]. Hence, the resultant intensity of electric field at the point P is
E=E1cosθ+E2cosθ
=14πε0q(r2+l2)cosθ+14πε0−q(r2+l2)cosθ
=14πε0q(r2+l2)2ocsθ
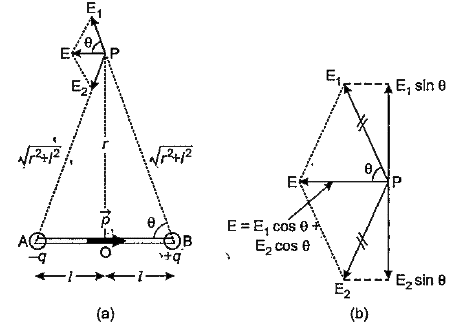
Now, from figure (a),
cosθ=BOBP
=l(r2+l2)1/2
∴E=14πε0q(r2+l2)2l(r2+l2)1/2
But 2ql=p (moment of electric dipole)
∴E=14πε0p(r2+l2)3/2
The direction of electric field E is .antiparallel to the dipole axis.
If r is very large compared to 2l(r>>2l), then l2 may be neglected in comparison to r2. Then, the electric field intensity at the point P due to the dipole is
E=14πε0pr3 Newton//Coulomb
Similar Questions
Obtain an expression for intensity of electric field in end on position, i.e., axial position of an electric dipole.
View SolutionAnswer the following:
(a) Derive and expression for the electric field at any point on the equatorial line of an electric dipole.
(b) Two identical point charges, q each kept 2m apart in air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View Solution(i) Derive the expression for electric field at a point on the equatorial line of an electric dipole.
(ii) Depiet the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
View SolutionWrite an expression (derivation not required) for intensity of electric field in :
(1) Axial position.
(2) Broad side position of an electric dipole, in terms of its length (2a) dipole moment (p) and distance (r).
(ii) What is the ratio of these two intensities i.e., E1:E2, for a short electric dipole ?
View Solution(a) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
(b) Derive an expression for the electric potential at any point along the axial line of an electric dipole
View Solution(a) Define electric dipole moment. Is it a scalar or a vector ? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
View SolutionElectric Field due to Dipole
View SolutionThe SI unit of electric field intensity is
View SolutionWrite an expression of magnetic flux density .B. at a point in end-on position or an axial position of a magnetic dipole. (Derivation not required.)
View Solution