Voltage applied between cathode and anode of an X-ray tube is 18 kV. Calculate the minimum wavelength of the X-rays produced.
To solve the problem of calculating the minimum wavelength of the X-rays produced in an X-ray tube with a voltage of 18 kV, we can follow these steps:
1. Understand the Formula:
The minimum wavelength (λmin) of the X-rays produced can be calculated using the formula:
λmin=h⋅ce⋅V
where:
- h is Planck's constant (6.63×10−34Js),
- c is the speed of light (3×108m/s),
- e is the charge of an electron (1.6×10−19C),
- V is the voltage (in volts).
2. Convert Voltage:
The voltage given is 18 kV, which needs to be converted to volts:
V=18kV=18×103V=18000V
3. Substitute Values into the Formula:
Now, substitute the values into the formula:
λmin=(6.63×10−34Js)⋅(3×108m/s)(1.6×10−19C)⋅(18000V)
4. Calculate the Denominator:
First, calculate the denominator:
e⋅V=(1.6×10−19C)⋅(18000V)=2.88×10−15J
5. Calculate the Numerator:
Now calculate the numerator:
h⋅c=(6.63×10−34Js)⋅(3×108m/s)=1.989×10−25Jm
6. Final Calculation:
Now, substitute the values back into the equation:
λmin=1.989×10−25Jm2.88×10−15J≈6.90×10−11m
7. Convert to Nanometers:
To express the wavelength in nanometers:
λmin≈6.90×10−11m=0.069nm
Final Answer:
The minimum wavelength of the X-rays produced is approximately 6.90×10−11m or 0.069nm.
The minimum wavelength (λmin) of the X-rays produced can be calculated using the formula:
λmin=h⋅ce⋅V
where:
- h is Planck's constant (6.63×10−34Js),
- c is the speed of light (3×108m/s),
- e is the charge of an electron (1.6×10−19C),
- V is the voltage (in volts).
The voltage given is 18 kV, which needs to be converted to volts:
V=18kV=18×103V=18000V
Now, substitute the values into the formula:
λmin=(6.63×10−34Js)⋅(3×108m/s)(1.6×10−19C)⋅(18000V)
First, calculate the denominator:
e⋅V=(1.6×10−19C)⋅(18000V)=2.88×10−15J
Now calculate the numerator:
h⋅c=(6.63×10−34Js)⋅(3×108m/s)=1.989×10−25Jm
Now, substitute the values back into the equation:
λmin=1.989×10−25Jm2.88×10−15J≈6.90×10−11m
To express the wavelength in nanometers:
λmin≈6.90×10−11m=0.069nm
The minimum wavelength of the X-rays produced is approximately 6.90×10−11m or 0.069nm.
Similar Questions
An X-ray tube is operated at 50 kV. The minimum wavelength produced is
View SolutionThe potential difference between the cathode. And the target electrod in a coolidge tube is 24.75 kV. The minimum wavelength of the emitted X-rays is
View SolutionThe voltage applied to an X-ray tube is 20 kV. The minimum wavelength of X-ray produced, is given by 31×n50Å then n will be
(h=6.62×10−34Jx,c=3×108m/s,e=1.6×10−19 coulomb):
View SolutionAn X-ray tube is operated at 20 kV. The cut off wavelength is
View SolutionOn operating an X-ray tube at 1 kV. X-rays of minimum wavelength 6.22Å are producd. I fht tube is operated at 10kV, then the minimum wavelength of X-rays prodcued will be
View SolutionThe distance between the cathode (filament) and the target in an X-ray tube is 1.5 m. If the cutoff wavelength is 30 pm, find the electric field between the cathode and the target.
View SolutionFigure below shows a simple diagram of a modern X ray tube. (i.e. Coolidge tube).
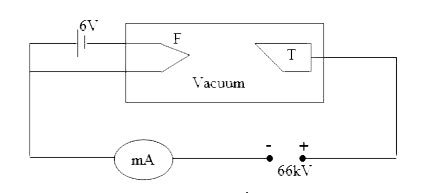
(i) Find the minimum wavelength of the X rays emitted by the X ray tube.
(ii) What will be the effect of replacing the 6V battery with a 9V battery on the emitted X rays?
View SolutionThe voltage applied to an X-ray tube is 18 kV. The maximum mass of phton emitted by the X-ray tube will be
View SolutionAtomic number of anti cathode material in an X- ray tube is 41. Wavelength of Ka X-ray produced in the tube is
View SolutionIf the potential difference between the anode and cathode of the X - ray tube is increases

View Solution

