When two thin lenses of focal lengths fi and f, are kept coaxially and in contact, prove that their cobined focal length "f" is given by :
1f=1f1+1f2
To prove that the combined focal length f of two thin lenses in contact with focal lengths f1 and f2 is given by the formula:
1f=1f1+1f2
we will follow these steps:
Step 1: Understanding the Setup
Consider two thin lenses L1 and L2 with focal lengths f1 and f2 respectively, placed coaxially and in contact with each other. An object is placed at a distance u from the first lens L1.
Hint: Visualize the arrangement of the lenses and the object to understand how light travels through them.
Step 2: Image Formation by the First Lens
Using the lens formula for the first lens L1:
1v′−1u=1f1
where v′ is the image distance from the first lens.
Hint: Remember that v′ can be positive or negative depending on the nature of the image formed (real or virtual).
Step 3: Virtual Object for the Second Lens
The image formed by the first lens L1 acts as a virtual object for the second lens L2. The distance of this virtual object from lens L2 is v′. Now, applying the lens formula for the second lens L2:
1v−1v′=1f2
where v is the final image distance from the second lens.
Hint: Keep track of the sign conventions for distances as you analyze the image formation.
Step 4: Adding the Two Equations
Now, we have two equations:
1. From lens L1:
1v′−1u=1f1(Equation 1)
2. From lens L2:
1v−1v′=1f2(Equation 2)
Adding these two equations:
(1v−1u)=1f1+1f2
Hint: When adding the equations, ensure that you correctly combine the fractions.
Step 5: Relating to the Combined Focal Length
The left side of the equation can be rewritten in terms of the combined focal length f:
1f=1v−1u
Thus, we can equate:
1f=1f1+1f2
Hint: This final step shows how the combined focal length relates to the individual focal lengths.
Conclusion
We have derived the formula for the combined focal length of two thin lenses in contact:
1f=1f1+1f2
This completes the proof.
Consider two thin lenses L1 and L2 with focal lengths f1 and f2 respectively, placed coaxially and in contact with each other. An object is placed at a distance u from the first lens L1.
Using the lens formula for the first lens L1:
The image formed by the first lens L1 acts as a virtual object for the second lens L2. The distance of this virtual object from lens L2 is v′. Now, applying the lens formula for the second lens L2:
Now, we have two equations:
1v′−1u=1f1(Equation 1)
1v−1v′=1f2(Equation 2)
The left side of the equation can be rewritten in terms of the combined focal length f:
We have derived the formula for the combined focal length of two thin lenses in contact:
Similar Questions
Knowledge Check
A plano convex lens has focal length f=20cm. If its plane surface is silvered, then new focal length will be
A20cmB40 cmC30 cmD10 cm
Two thin lenses of focal length f1 and f2 are in contact and coaxial. The power of the combination is
View SolutionTwo thin lenses, one of focal length + 60 cm and the other of focal length – 20 cm are put in contact. The combined focal length is
View SolutionTwo similar thin equi-convex lenses, of focal f each, are kept coaxially in contact with each other such that the focal length of the combination is F1, When the space between the two lens is filled with glycerin (which has the same refractive index (μ=1.5) as that of glass) then the equivlent focal length is F2, The ratio F1:F2 will be
View SolutionA convex lens of focal length f cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown:
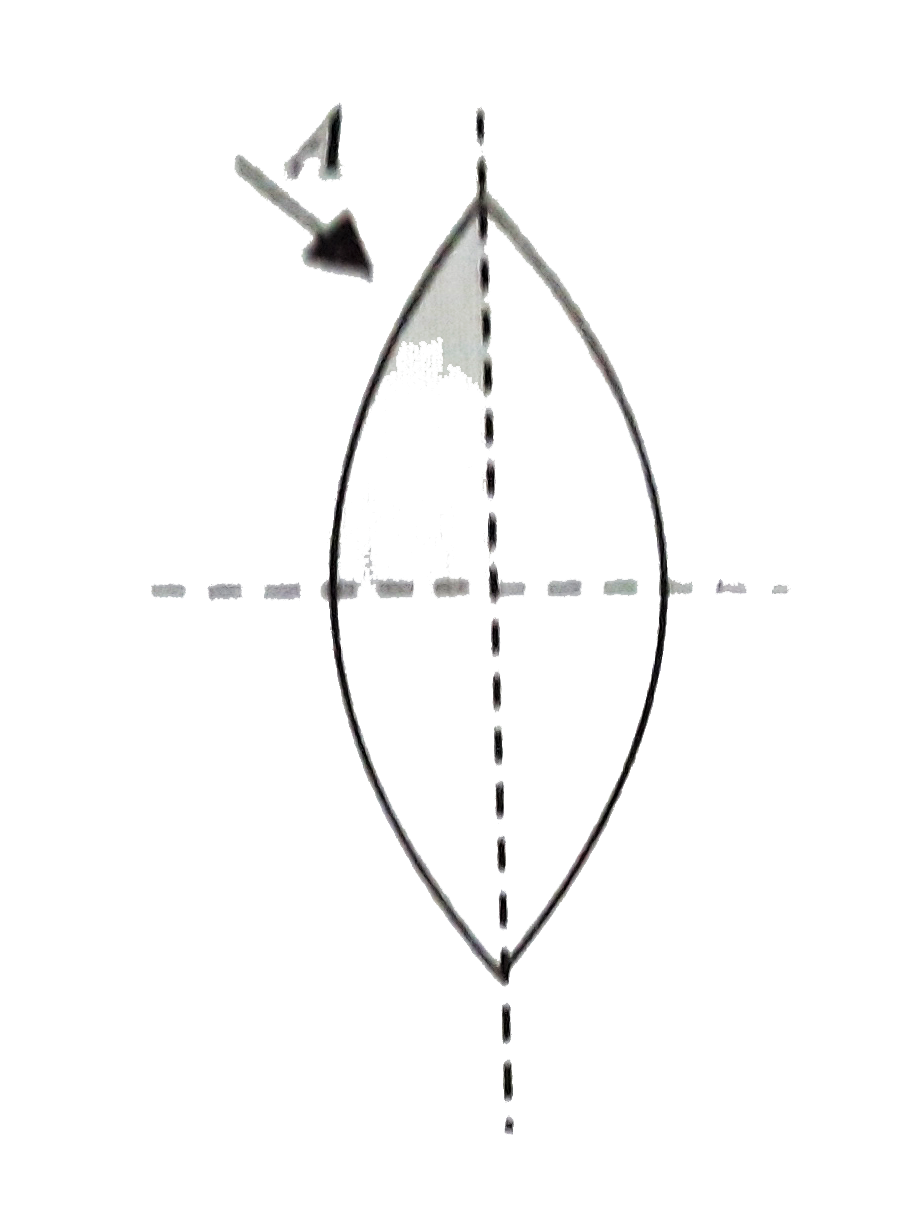
View SolutionA convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
View Solution(a) Using the ray diagram for a system of two lenses of focal lengths f1andf2 in contact with each other, show that the two lens system can be regarded as equivalent to a single lens of focal length f, where
1f=1f1+1f2
Also write the relation for the equivalent power of the lens combination.
(b) Determine the position of the image formed by the lens combination given in the figure.
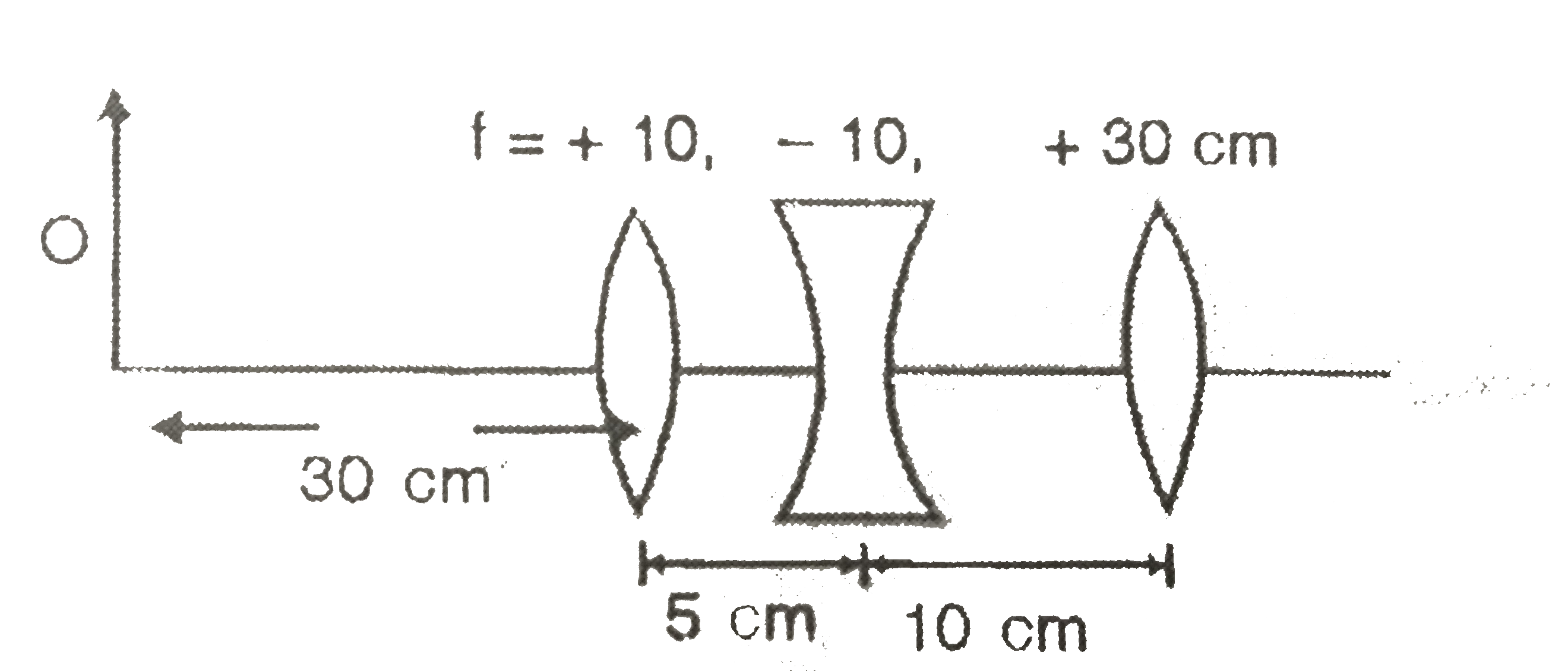
View SolutionAn object is placed in front of a converging lens at a distance equal to twice the focal length f1 of the lens. On the other side of the lens is a concave mirror of focal length f2 separated from the lens is a concave mirror of focal length f2 separated from the lens by a distance 2(f1+f2). Light from the object passes rightward through the lens, reflects from the mirror, passes leftward throught the lens, and forms a final image of the object.

View Solution

