Question

Obtain an expression for equivalent capacitance when three capacitors $C_1,C_2\text{and}{C}_3$ are connected in series.

Explanation

Let three capacitors `C_(1),C_(2)` and `C_(3)` are connected in series. We know charge remains same in series combination.

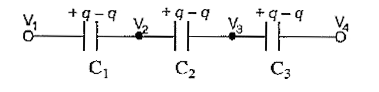
`V_(1)=(q)/(C_(1))`
`V_(2)=(q)/(C_(2))`
`V_(3)=(q)/(C_(3))`
`V=V_(1)+V_(2)+V_(3)`
`=q((1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3)))`
If the 3 capacitors are replaced by a single capacitor such that on giving it charge q, a capacitance C is obtained then `V=(q)/(C)`
`:.(q)/(C)=q((1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3)))`
or `(1)/(C)=(1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3))`