The elevation of boiling point produced by dilute equimolal solutions of three substances are in the order A>glucose>B Suggest a reason for this observation.
To solve the problem regarding the elevation of boiling points produced by dilute equimolal solutions of three substances (A, glucose, and B), we can follow these steps:
1. Understanding Elevation of Boiling Point:
The elevation of boiling point (ΔTb) is given by the formula:
ΔTb=i⋅Kb⋅m
where:
- i = van 't Hoff factor (number of particles the solute dissociates into)
- Kb = ebullioscopic constant of the solvent
- m = molality of the solution
2. Equimolal Solutions:
Since the solutions are equimolal, the molality (m) is the same for all three substances (A, glucose, and B). Therefore, the difference in boiling point elevation will depend on the van 't Hoff factor (i).
3. Analyzing the Substances:
- Glucose: Glucose is a non-electrolyte and does not dissociate in solution. Thus, its van 't Hoff factor i is equal to 1.
- Substance A: The problem states that A produces a greater elevation in boiling point than glucose, indicating that A must dissociate into more particles in solution. Therefore, iA>1.
- Substance B: B produces a lesser elevation in boiling point than glucose, suggesting that B associates in solution, leading to fewer particles than expected. Thus, iB<1.
4. Conclusion:
Based on the above analysis, we can conclude that:
- A has a higher van 't Hoff factor (iA>1) due to dissociation, leading to a greater elevation of boiling point.
- Glucose has a van 't Hoff factor of 1 because it does not dissociate.
- B has a lower van 't Hoff factor (iB<1) due to association, resulting in a lower elevation of boiling point.
Thus, the order of elevation of boiling points is:
A>glucose>B
The elevation of boiling point (ΔTb) is given by the formula:
ΔTb=i⋅Kb⋅m
where:
- i = van 't Hoff factor (number of particles the solute dissociates into)
- Kb = ebullioscopic constant of the solvent
- m = molality of the solution
Since the solutions are equimolal, the molality (m) is the same for all three substances (A, glucose, and B). Therefore, the difference in boiling point elevation will depend on the van 't Hoff factor (i).
- Glucose: Glucose is a non-electrolyte and does not dissociate in solution. Thus, its van 't Hoff factor i is equal to 1.
- Substance A: The problem states that A produces a greater elevation in boiling point than glucose, indicating that A must dissociate into more particles in solution. Therefore, iA>1.
- Substance B: B produces a lesser elevation in boiling point than glucose, suggesting that B associates in solution, leading to fewer particles than expected. Thus, iB<1.
Based on the above analysis, we can conclude that:
- A has a higher van 't Hoff factor (iA>1) due to dissociation, leading to a greater elevation of boiling point.
- Glucose has a van 't Hoff factor of 1 because it does not dissociate.
- B has a lower van 't Hoff factor (iB<1) due to association, resulting in a lower elevation of boiling point.
A>glucose>B
Topper's Solved these Questions
- SOLUTIONSBOOK - ICSECHAPTER - SOLUTIONSEXERCISE - ISC EXAMINATION QUESTIONS (PART-II Descriptive Questions) (Numerical Problems)
14 Videos
- SOLUTIONSBOOK - ICSECHAPTER - SOLUTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS
23 Videos
- SOLUTIONSBOOK - ICSECHAPTER - SOLUTIONSEXERCISE - ISC EXAMINATION QUESTIONS (PART-I Objective Questions) (Choose the correct alternative)
8 Videos
- SOLID STATEBOOK - ICSECHAPTER - SOLID STATEEXERCISE - ISC EXAMINATION QUESTIONS PART-I (Numerical Problems)
6 Videos
- SOME IMPORTANT ORGANIC NAME REACTIONS BOOK - ICSECHAPTER - SOME IMPORTANT ORGANIC NAME REACTIONS EXERCISE - Questions
278 Videos
Similar Questions
Assertion (A): The elevation in boiling point for two isotonic solutions may not be same.
Reason (R ): The boiling point depends upon the concentration of the solute.
View SolutionCalculate elevation in boiling point for 2 molal aqueous solution of glucose.
(Given Kb(H2O)=0.5kgmol−1)
View SolutionElevation in the boiling point for 1 molal solution of glucose is 2K. The depression in the freezing point for 2 molal solution of glucose in the same solvent is 2K. The relation between KbandKf is
View SolutionFor [CrCl3.xNH3], elevation in boiling point of one molal solution is double of one molal solution of glucose , hence x is if complex is 100% ionised :
View SolutionWhen a substance A reacts with water it produces a combustible gas B and a solution of substance C in water. When another substance D reacts with this solution of C, it also produces the same gas B on warming but D can produce gas B on reaction with dilute sulphuric acid at room temperature. A imparts a deep golden yellow colour a smokeless flame to Bunsen burner. A,B,C, and D respectively are :
View SolutionElevation in boiling point of an aqueous solution of urea is 0.52(kbfor water=0.52Kmolality−1). The mole fraction of urea in this solution is :
View SolutionAssertion Boiling point of halogen acids are in the order HF>HBr>HCl>HI
Reasoning Electronegativities are in the order F>Cl>Br>I .
View Solution(a) A solution containing 0.5g of naphithalene in 50gCCl4 yield a boiling point elevation of 0.4K, while a solution of 0.6g of an unknown solute in the same mass of the solvent gives a boiling point elevation of 0.65K. Find the molar mass of the unknown solute.
(b) The boiling point of a solution of 0.1g of a substance in 16g of ether was found to be 0.100∘C higher that of pure ether. What is the molecular mass of the substance. Kb (ether) =2.16Kkgmol−1
View SolutionIf the elevation in boiling point of a solution of 10 g of solute (molecular weight = 100) in 100 g of water is ΔTb, the ebullioscopic constant of water is
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
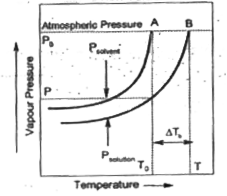
Variation of vapour pressure with temperature and showing elevation in boiling point.
Elevation in boiling point of an aqueous urea solution is 0.52∘.(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:
View Solution
