A lever has fulcrum and load at the ends and effort in between them. Draw diagram and state whether the velocity ratio of the lever is greater, equal or less than 1 ? Can the velocity ratio of this lever be changed?
Step-by-Step Solution:
1. Understanding the Lever Arrangement:
- A lever consists of three main components: the fulcrum (pivot point), the load (weight being lifted), and the effort (force applied).
- In this scenario, the fulcrum is at one end, the load is at the other end, and the effort is applied in between them.
2. Drawing the Diagram:
- Draw a horizontal line to represent the lever.
- Mark the left end as the fulcrum (F).
- Mark the right end as the load (L).
- Mark a point between F and L as the effort (E).
- Label the distances: let the distance from F to E be the effort arm (d1) and the distance from E to L be the load arm (d2).
F(Fc–rum)−−−−−E(Effort)−−−−−L(Load)
3. Calculating the Velocity Ratio (VR):
- The velocity ratio (VR) of a lever is defined as the ratio of the length of the effort arm to the length of the load arm.
- Mathematically, it can be expressed as:
\(
\text{Velocity Ratio (VR)} = \frac{\text{Effort Arm (d1)}}{\text{Load Arm (d2)}}
\)
- In this case, since the effort arm (d1) is shorter than the load arm (d2), we can conclude that:
\(
\text{VR} < 1
\)
4. Conclusion on Velocity Ratio:
- Since the effort arm is less than the load arm, the velocity ratio of this lever is less than 1.
- This indicates that the lever does not amplify the input speed; instead, it requires more effort to lift a smaller load.
5. Can the Velocity Ratio be Changed?:
- In this specific design of the lever, the velocity ratio cannot be changed because it is determined by the fixed positions of the fulcrum, load, and effort.
- To change the velocity ratio, one would need to alter the distances of the effort arm or the load arm, which is not possible in this arrangement.
- A lever consists of three main components: the fulcrum (pivot point), the load (weight being lifted), and the effort (force applied).
- In this scenario, the fulcrum is at one end, the load is at the other end, and the effort is applied in between them.
- Draw a horizontal line to represent the lever.
- Mark the left end as the fulcrum (F).
- Mark the right end as the load (L).
- Mark a point between F and L as the effort (E).
- Label the distances: let the distance from F to E be the effort arm (d1) and the distance from E to L be the load arm (d2).
- The velocity ratio (VR) of a lever is defined as the ratio of the length of the effort arm to the length of the load arm.
- Mathematically, it can be expressed as:
\(
\text{Velocity Ratio (VR)} = \frac{\text{Effort Arm (d1)}}{\text{Load Arm (d2)}}
\)
- In this case, since the effort arm (d1) is shorter than the load arm (d2), we can conclude that:
\(
\text{VR} < 1
\)
- Since the effort arm is less than the load arm, the velocity ratio of this lever is less than 1.
- This indicates that the lever does not amplify the input speed; instead, it requires more effort to lift a smaller load.
- In this specific design of the lever, the velocity ratio cannot be changed because it is determined by the fixed positions of the fulcrum, load, and effort.
- To change the velocity ratio, one would need to alter the distances of the effort arm or the load arm, which is not possible in this arrangement.
Topper's Solved these Questions
Similar Questions
A machine works as a (i) force multiplier, (ii) speed multiplier. In each case state whether the velocity ratio is more than or less than 1.
View SolutionA lever of length 9 cm has its load arm 5 cm long and the effort arm is 9 cm long. (a) to which class does it belong ?
(b) Draw a diagram of the lever showing the position of the fulcrum F and directions of both the load L and effort E. (c) what is the mechanical advantage and velocity ratio if the efficiency is 100%?
(d) What will be the mechanical advantage and velocity ratio if the efficiency becomes 50%?
View SolutionFigure, shows a uniform metre rule of weight W supported on a fulcrum at the 60 cm mark by applying the effort E at the 90 cm mark.
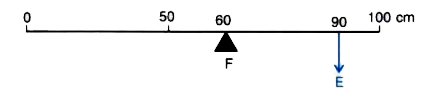
(a) State with reason whether the weight W of the rule is greater than, less than or equal to the effort E.
(b) Find the mechanical advantage in a ideal case.
View SolutionA concave lens always forms a virtual image. Draw a ray diagram to show it. State the magnification of the image with sign, whether greater than, equal to or less than 1.
View SolutionState one reason why mechanical advantage is less than the velocity ratio for an actual machine.
View Solution
What will always be true about the load/effort ratio of this type of lever ?
View SolutionHow is mechanical advantage related with velocity ratio for an actual machine ? State whether the efficiency of such a machine is equal to 1, les sthan 1 or more than 1.
View SolutionState the kind of lever which always has mechanical advantage less than 1. Draw a labelled diagram of such a lever.
View SolutionState whether the following statements are true or false by writing T or F.
(a) The velocity ratio of a single fixed pulley is always more than 1.
(b) The velocity ratio of a single movable pulley is always 2.
(c) The velocity ratio of a combination of n movable pulleys with a fixed pulley is always 2n.
(d) The velocity ratio of a block and tackle system is always equal to the number of strands of the tackle supporting the load.
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
if the first particle is stopped for a moment and then released, the velocity of center of mass of the system just after the release will be
View Solution
