ABC is an isosceles right-angled triangle. Assuming AB = BC = x, find the value of each of the following trigonometric ratios :

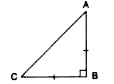
(i) ${sin 45}^{\circ}$
(ii) ${cos 45}^{\circ}$
(iii) ${tan 45}^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(i) $\frac{1}{\sqrt{2}} (ii) \frac{1}{\sqrt{2}} (iii) 1$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for ABC is an isosceles right-angled triangle. Assuming AB = BC = x, find the value of each of the following trigonometric ratios : (i) sin45^(@) (ii) cos45^(@) (iii) tan45^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS TRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(B)
34 Videos
TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(C)
118 Videos
TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(C)
118 Videos
TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -4 ( COMPLEMENTARY ANGLES ) (4 MARKS QUESTIONS )
4 Videos

ABC is an isosceles right-angled triangle. Assuming AB = BC = x, find the value of each of the following trigonometric ratios :

(i) ${sin 45}^{\circ}$
(ii) ${cos 45}^{\circ}$
(iii) ${tan 45}^{\circ}$

The correct Answer is:(i) $\frac{1}{\sqrt{2}} (ii) \frac{1}{\sqrt{2}} (iii) 1$

Topper's Solved these Questions

Similar Questions

ICSE-TRIGONOMETRICAL RATIOS OF STANDARD ANGLES-EXERCISE 23(A)

ABC is an isosceles right-angled triangle. Assuming AB = BC = x, find the value of each of the following trigonometric ratios : (i) sin45∘ (ii) cos45∘ (iii) tan45∘

The correct Answer is:(i) 1√2 (ii) 1√2 (iii) 1

Topper's Solved these Questions

Similar Questions

ICSE-TRIGONOMETRICAL RATIOS OF STANDARD ANGLES-EXERCISE 23(A)

ABC is an isosceles right-angled triangle. Assuming AB = BC = x, find the value of each of the following trigonometric ratios :

(i) ${sin 45}^{\circ}$
(ii) ${cos 45}^{\circ}$
(iii) ${tan 45}^{\circ}$

The correct Answer is:(i) $\frac{1}{\sqrt{2}} (ii) \frac{1}{\sqrt{2}} (iii) 1$