In the given figure, a square is inscribed in a circle with centre O. Find :
∠BOC .
Is BD a diameter of the circle
To solve the problem, we need to find the angle ∠BOC and determine if BD is a diameter of the circle.
1. Identify the Square and Circle:
We have a square inscribed in a circle with center O. The vertices of the square can be labeled as A,B,C,D in a clockwise manner.
2. Understand the Properties of the Square:
The diagonals of a square intersect each other at right angles (90 degrees). Thus, we can say:
∠COD=90∘
3. Extend the Lines:
Extend the line OB to point D and line OC to point A. This means that BD is a straight line.
4. Use the Straight Line Property:
Since BD is a straight line, the sum of angles on a straight line is 180∘. Therefore:
∠BOC+∠COD=180∘
5. Substitute the Known Angle:
We know from step 2 that ∠COD=90∘. Substituting this into the equation gives:
∠BOC+90∘=180∘
6. Solve for ∠BOC:
Rearranging the equation to find ∠BOC:
∠BOC=180∘−90∘=90∘
7. Determine if BD is a Diameter:
Since ∠BOC=90∘, and BD is a straight line, it confirms that BD is the diameter of the circle.
Conclusion:
Thus, we find that:
- ∠BOC=90∘
- BD is indeed the diameter of the circle.
We have a square inscribed in a circle with center O. The vertices of the square can be labeled as A,B,C,D in a clockwise manner.
The diagonals of a square intersect each other at right angles (90 degrees). Thus, we can say:
∠COD=90∘
Extend the line OB to point D and line OC to point A. This means that BD is a straight line.
Since BD is a straight line, the sum of angles on a straight line is 180∘. Therefore:
∠BOC+∠COD=180∘
We know from step 2 that ∠COD=90∘. Substituting this into the equation gives:
∠BOC+90∘=180∘
Rearranging the equation to find ∠BOC:
∠BOC=180∘−90∘=90∘
Since ∠BOC=90∘, and BD is a straight line, it confirms that BD is the diameter of the circle.
Thus, we find that:
- ∠BOC=90∘
- BD is indeed the diameter of the circle.
Topper's Solved these Questions
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(B)
Explore 15 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:DISTANCE FORMULA
Explore 11 Videos
- CIRCLES Book:ICSEChapter:CIRCLES Exercise:TOPIC-2
Explore 25 Videos
Similar Questions
In the given figure, a square is inscribed in a circle with centre O. Find :
∠OCB . Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠BOD .Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠COD . Is BD a diameter of the circle
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠BOC
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠OBC
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
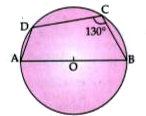
∠BCD=130∘. Find
(i) ∠DAB
View SolutionA square is inscribed in a circle of radius 7 cm. Find the area of the square.
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
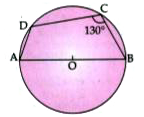
∠BCD=130∘. Find
(ii) ∠DBA
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
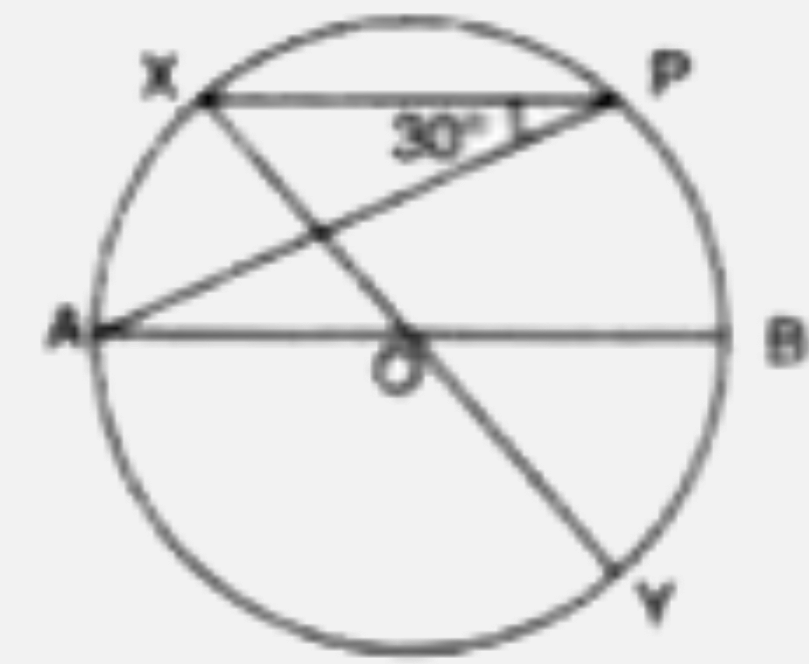
∠OAX
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠BPY
View Solution

