State, with reason which of the are surds and which are not :
The correct Answer is:not a surd as is irrational
To determine whether √π is a surd or not, we can follow these steps:
Step 1: Understand the definition of a surd
A surd is an expression containing a root (such as a square root) that cannot be simplified to remove the root. This typically occurs when the number under the root is irrational.
Step 2: Identify the nature of π
The number π is known to be an irrational number. This means that it cannot be expressed as a fraction of two integers, and its decimal representation is non-terminating and non-repeating.
Step 3: Analyze √π
Since π is irrational, when we take the square root of π, we are left with √π. There is no way to simplify √π into a rational number because π itself does not have a rational square root.
Step 4: Conclusion
Since √π contains an irrational number under the radical sign and cannot be simplified to remove the radical, we conclude that √π is indeed a surd.
Final Answer:
√π is a surd because it contains an irrational number under the radical sign, which cannot be simplified.
---
A surd is an expression containing a root (such as a square root) that cannot be simplified to remove the root. This typically occurs when the number under the root is irrational.
The number π is known to be an irrational number. This means that it cannot be expressed as a fraction of two integers, and its decimal representation is non-terminating and non-repeating.
Since π is irrational, when we take the square root of π, we are left with √π. There is no way to simplify √π into a rational number because π itself does not have a rational square root.
Since √π contains an irrational number under the radical sign and cannot be simplified to remove the radical, we conclude that √π is indeed a surd.
√π is a surd because it contains an irrational number under the radical sign, which cannot be simplified.
Topper's Solved these Questions
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (B)
43 Videos
- PYTHAGORAS THEOREMBOOK - ICSECHAPTER - PYTHAGORAS THEOREMEXERCISE - 4 MARKS QUESTIONS
9 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - QUADRILATERALS AND ITS PROPERTIES - 4 MARKS QUESTIONS
7 Videos
Similar Questions
State, with reason which of the are surds and which are not :
√180
View SolutionState, with reason which of the are surds and which are not :
√3+√2
View SolutionState, with reason which of the are surds and which are not :
4√27
View SolutionState, with reason which of the are surds and which are not :
3√−125
View SolutionState, with reason, which of the following are surds and which are not :
(i) √180 (ii) 3√64 (iii) 3√25×3√40
View SolutionState with reasons which of the following is a surd which is not :
(i) √27 (ii) √225×√4
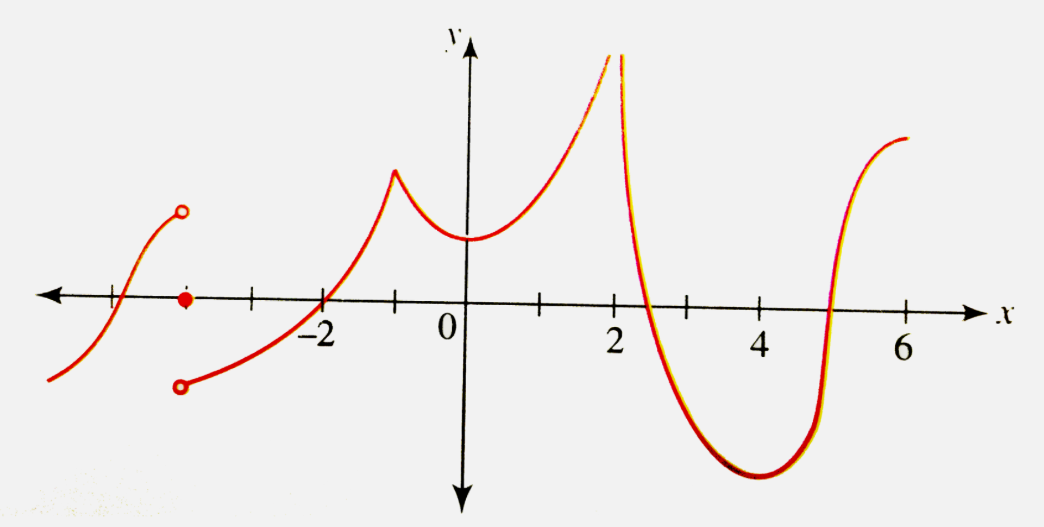
View SolutionThe graph of f is shown. State, with reason, the numbers at which f is not differentiable.
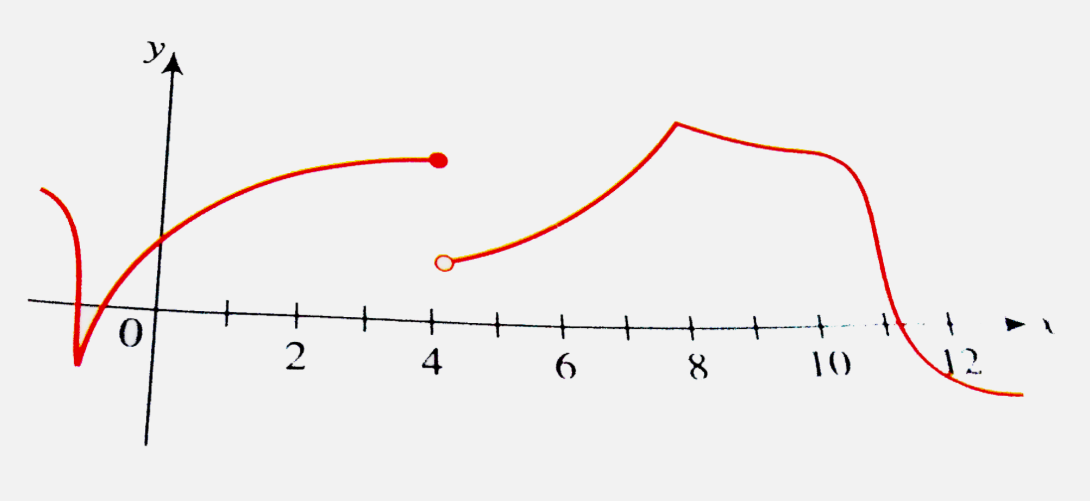
View SolutionThe graph of f(x) is given. State with reasons the number at which the function is non-differentiable.
View SolutionState the factors which affect the atomic size of elements in a periodic table. In period 2 from left to right, state which element has the largest atomic size and which has the smallest, giving reasons.
View SolutionState with reasons :
(i) Which is more acidic : anhydrous HCl or aqueous HCl ?
(ii) Which is more polar : CO2orN2O ?
(iii) Which is more soluble in water : enhyl alcohol or dimethyl ether ?
View Solution
