In ΔABC,∠B=90∘andAEandCF are the angle bisector (line segments that divide an angle into two equal parts) of ∠Aand∠C, respectively. Find ∠ADC.
The correct Answer is:∠ADC=135∘.
To find the angle ∠ADC in triangle ABC where ∠B=90∘ and AE and CF are the angle bisectors of ∠A and ∠C respectively, we can follow these steps:
Step 1: Understand the Properties of Triangle ABC
In triangle ABC:
- ∠B=90∘
- The sum of angles in a triangle is 180∘.
Step 2: Use the Angle Sum Property
Using the angle sum property of triangle ABC:
∠A+∠B+∠C=180∘
Substituting ∠B=90∘:
∠A+90∘+∠C=180∘
This simplifies to:
∠A+∠C=90∘
Step 3: Define the Angles Created by the Angle Bisectors
Let:
- ∠A=1+2 (where AE is the angle bisector, so 1=2)
- ∠C=3+4 (where CF is the angle bisector, so 3=4)
From the angle bisector properties, we have:
1=2and3=4
Step 4: Substitute the Angle Bisector Values
Since ∠A+∠C=90∘, we can write:
(1+1)+(3+3)=90∘
This simplifies to:
2⋅1+2⋅3=90∘
Thus:
2(1+3)=90∘
Dividing by 2:
1+3=45∘
So, we conclude:
∠1+∠3=45∘
Step 5: Apply the Angle Sum Property in Triangle ADC
In triangle ADC:
∠2+∠4+∠ADC=180∘
Substituting ∠2=1 and ∠4=3:
1+3+∠ADC=180∘
From our previous result, we know 1+3=45∘:
45∘+∠ADC=180∘
Step 6: Solve for Angle ADC
Now, isolate ∠ADC:
∠ADC=180∘−45∘=135∘
Final Answer
Thus, the measure of ∠ADC is:
∠ADC=135∘
---
In triangle ABC:
- ∠B=90∘
- The sum of angles in a triangle is 180∘.
Using the angle sum property of triangle ABC:
∠A+∠B+∠C=180∘
Substituting ∠B=90∘:
∠A+90∘+∠C=180∘
This simplifies to:
∠A+∠C=90∘
Let:
- ∠A=1+2 (where AE is the angle bisector, so 1=2)
- ∠C=3+4 (where CF is the angle bisector, so 3=4)
1=2and3=4
Since ∠A+∠C=90∘, we can write:
(1+1)+(3+3)=90∘
This simplifies to:
2⋅1+2⋅3=90∘
Thus:
2(1+3)=90∘
Dividing by 2:
1+3=45∘
So, we conclude:
∠1+∠3=45∘
In triangle ADC:
∠2+∠4+∠ADC=180∘
Substituting ∠2=1 and ∠4=3:
1+3+∠ADC=180∘
From our previous result, we know 1+3=45∘:
45∘+∠ADC=180∘
Now, isolate ∠ADC:
∠ADC=180∘−45∘=135∘
Thus, the measure of ∠ADC is:
∠ADC=135∘
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBook:ICSEChapter:THE TRIANGLE AND ITS PROPERTIESExercise:EXERCISE 12.1
Explore 7 Videos
- THE TRIANGLE AND ITS PROPERTIESBook:ICSEChapter:THE TRIANGLE AND ITS PROPERTIESExercise:EXERCISE 12.2
Explore 11 Videos
- THE TRIANGLE AND ITS PROPERTIESBook:ICSEChapter:THE TRIANGLE AND ITS PROPERTIESExercise:WARM UP EXERCISE
Explore 3 Videos
- SYMMETRYBook:ICSEChapter:SYMMETRYExercise:Exercise 19B
Explore 13 Videos
- UNITARY METHODBook:ICSEChapter:UNITARY METHODExercise:EXERCISE
Explore 16 Videos
Similar Questions
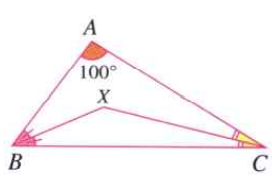
In ΔABC,∠=100∘. Line segment BX divides ∠B into two equal parts and CX divides ∠C into two equal parts. Find ∠BXC.
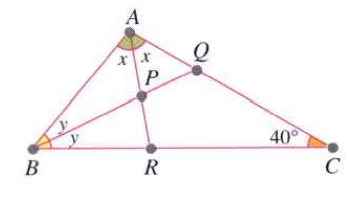
View SolutionIn ΔABC,∠C=40∘,BQandAR are the angle bisectors of ∠Band∠A, respectively. Find ∠APQ.
View SolutionIn ΔABC,∠B=90∘,∠A=30∘,b=20cm, find a and c.
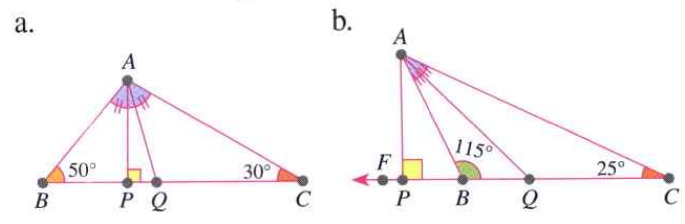
View SolutionIn ΔABC,AP⊥BCandAQ is the angle bisector of ∠BAC. Find ∠PAQ.
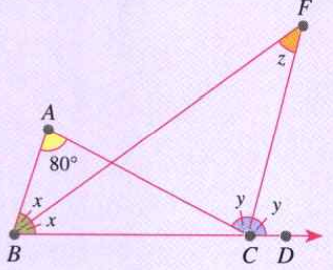
View SolutionIn ΔABC,∠A=80∘, the bisectors of ∠ABCand∠ACD meet at point F. find angle z?
View SolutionIn ΔABC,∠B=90∘andsinA=45, then find the values of all other trigonometric ratios for ∠A.
View SolutionInΔABC,∠B=90∘andcosA=941, then find all other trigonometric ratios for ∠A.
View SolutionABCD is a parallelogram and AE and CF bisect ∠Aand∠C respectively. Prove that AE||FC.

View SolutionIn ΔABC,∠B=90∘andsinA=35, then find all other trigonometric ratios for ∠A.
View SolutionIn ΔABC,∠A=90∘andtanB=56, then find all other trigonometric ratios for ∠B.
View Solution

