Jessica draws an isosceles triangle. The length of each of the two equal sides is twice as much as the length of the base. If the length of the base is x, find the rule for finding the perimeter of the triangle.
The correct Answer is:5x
To find the rule for finding the perimeter of the isosceles triangle drawn by Jessica, we will follow these steps:
1. Identify the lengths of the sides:
- Let the length of the base (BC) be represented as x.
- Since the triangle is isosceles, the lengths of the two equal sides (AB and AC) are each twice the length of the base. Therefore, we can express the lengths of the equal sides as:
- AB=2x
- AC=2x
2. Write the formula for the perimeter:
- The perimeter P of a triangle is the sum of the lengths of all its sides. Thus, we can write:
P=AB+BC+AC
3. Substitute the values of the sides into the perimeter formula:
- Substitute AB=2x, BC=x, and AC=2x into the perimeter formula:
P=2x+x+2x
4. Combine like terms:
- Now, combine the terms:
P=2x+2x+x=5x
5. State the final rule for the perimeter:
- Therefore, the rule for finding the perimeter of the triangle is:
P=5x
Final Answer:
The rule for finding the perimeter of the triangle is P=5x.
- Let the length of the base (BC) be represented as x.
- Since the triangle is isosceles, the lengths of the two equal sides (AB and AC) are each twice the length of the base. Therefore, we can express the lengths of the equal sides as:
- AB=2x
- AC=2x
- The perimeter P of a triangle is the sum of the lengths of all its sides. Thus, we can write:
P=AB+BC+AC
- Substitute AB=2x, BC=x, and AC=2x into the perimeter formula:
P=2x+x+2x
- Now, combine the terms:
P=2x+2x+x=5x
- Therefore, the rule for finding the perimeter of the triangle is:
P=5x
The rule for finding the perimeter of the triangle is P=5x.
Similar Questions
In an isosceles triangle, each of the two equal sides is 10cm less than three times the base. If the perimeter of the triangle is 330cm, find the lengths of the sides of the triangle.
View SolutionThe perimeter of an isosceles triangle is 49 m and the length of one of its equal sides is 17m. Find the length of the base of the triangle.
View SolutionThe area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm is
View SolutionDraw an isosceles triangle in which each of the equal sides is of length 3 cm and the angle between them is450.
View SolutionIf the length of two sides of an isosceles triangle are 3 and 7, what is the perimeter of the triangle?
View SolutionFind the perimeter of an isosceles triangle with each of the equal sides 17 cm and base 15 cm.
View SolutionAn isosceles triangle has base 20cm and each of the two equal sides measures 18 cm. What is its perimeter?
View SolutionFind the length of the third side of the triangle.
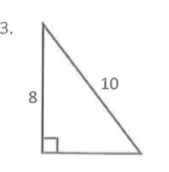
View SolutionFind the length of the third side of the triangle.
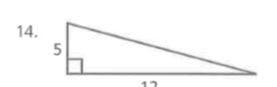
View SolutionAn isosceles triangle has perimeter 30cm and each of the equal sides os 12 cm. Find the area of the triangle.
View Solution

