Write the rule that gives the number of matchsticks required to make a pattern of letter M.
The correct Answer is:4n where n = number of letters used for making the pattern
To determine the number of matchsticks required to create the letter "M," we can follow these steps:
1. Identify the Structure of the Letter "M":
The letter "M" consists of two vertical lines and two diagonal lines connecting them.
2. Count the Matchsticks:
- First Vertical Line: We need 1 matchstick for the left vertical line.
- Second Vertical Line: We need another matchstick for the right vertical line.
- First Diagonal Line: We need 1 matchstick for the diagonal line going from the bottom of the left vertical line to the top of the right vertical line.
- Second Diagonal Line: We need another matchstick for the diagonal line going from the top of the left vertical line to the bottom of the right vertical line.
3. Total Matchsticks Calculation:
- Adding them up:
- 1 (left vertical) + 1 (right vertical) + 1 (first diagonal) + 1 (second diagonal) = 4 matchsticks.
4. Formulate the Rule:
- Since we consistently use 4 matchsticks to create the letter "M," we can express this as a rule:
- The number of matchsticks required to create the letter "M" can be represented as:
Number of matchsticks=4
- If we generalize this for "n" letters "M," the formula would be:
Total matchsticks for n letters=4n
Final Answer:
The number of matchsticks required to make the letter "M" is 4. The rule can be expressed as 4n, where n is the number of letters "M."
---
The letter "M" consists of two vertical lines and two diagonal lines connecting them.
- First Vertical Line: We need 1 matchstick for the left vertical line.
- Second Vertical Line: We need another matchstick for the right vertical line.
- First Diagonal Line: We need 1 matchstick for the diagonal line going from the bottom of the left vertical line to the top of the right vertical line.
- Second Diagonal Line: We need another matchstick for the diagonal line going from the top of the left vertical line to the bottom of the right vertical line.
- Adding them up:
- 1 (left vertical) + 1 (right vertical) + 1 (first diagonal) + 1 (second diagonal) = 4 matchsticks.
- Since we consistently use 4 matchsticks to create the letter "M," we can express this as a rule:
- The number of matchsticks required to create the letter "M" can be represented as:
Number of matchsticks=4
- If we generalize this for "n" letters "M," the formula would be:
Total matchsticks for n letters=4n
The number of matchsticks required to make the letter "M" is 4. The rule can be expressed as 4n, where n is the number of letters "M."
Similar Questions
Write the rule that gives the number of matchsticks required to make the following pattern.

View SolutionFind a rule which gives the number of matchsticks required to make a pattern of the letter E as E
View SolutionFind the rule which gives the number of matchsticks required to make a pattern of n such shapes.
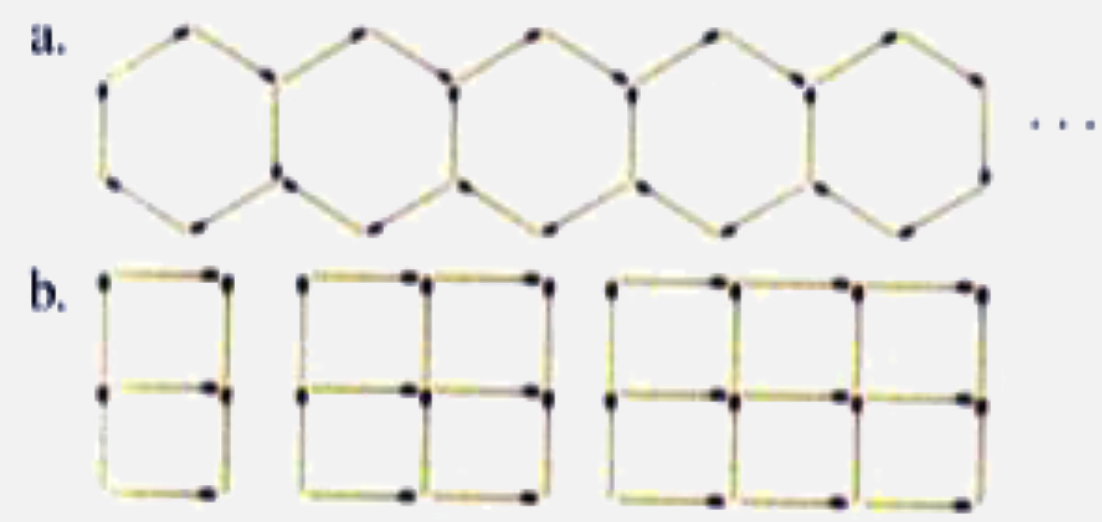
View SolutionFind the rule that gives the number of matchsticks required to make the following pattern. Also, find the number of matchsticks required to make a pattern of 9 diamonds.

View SolutionFind the rule that gives the number of matchsticks required to build the following pattern. Also find the number of matchsticks required to make a pattern with 6 squares at the base.
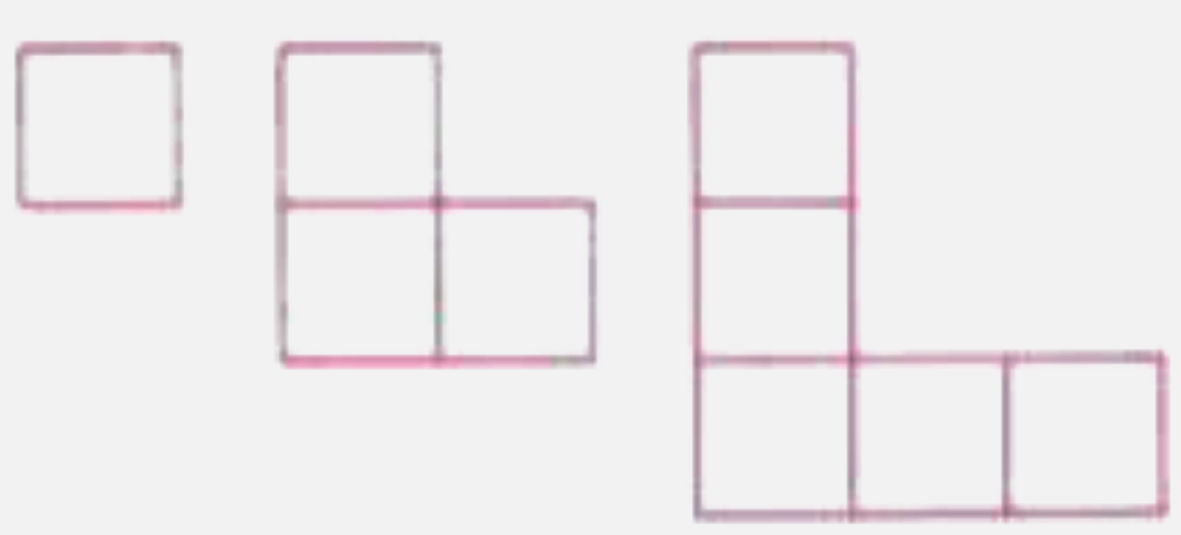
View SolutionFind the rule which gives the number of matchsticks required to make thefollowing matchstick patterns. Use a variable to write the rule.(a) A pattern of letter T as(b) A pattern of letter Z as(c) A pattern of letter U as(d) A pattern of letter V as(e) A pattern of letter E as(f) A pattern of letter S as(g) A pattern of letter A as
View SolutionFind a rule that gives the number of line segments required to make the following pattern.

View Solution(a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.)(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
View SolutionLook at the following matchstick pattern of squares. The squares are not separate. Two neighboring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint: If you remove the vertical stick at the end, you will get a pattern of Cs.)
View SolutionFind a rule that gives the number of line segments required to make the following pattern of squares.

View Solution
