Using truth table , prove that :(p→q)→[(~p→q)→q] is a tautology.
The correct Answer is:(i) Some circles are not round .
(ii) The set of prime numbers is finite.
To prove that the expression (p→q)→((¬p→q)→q) is a tautology using a truth table, we will follow these steps:
Step 1: Set Up the Truth Table
We will create a truth table with columns for p, q, ¬p, p→q, ¬p→q, (¬p→q)→q, and finally (p→q)→((¬p→q)→q).
| p | q | ¬p | p→q | ¬p→q | (¬p→q)→q | (p→q)→((¬p→q)→q) |
|-------|-------|------------|--------------|-------------------|---------------------------|------------------------------------------|
| T | T | F | T | T | T | T |
| T | F | F | F | T | F | T |
| F | T | T | T | T | T | T |
| F | F | T | T | F | F | T |
Step 2: Fill in the Values
1. Column for p and q: List all combinations of truth values for p and q (True (T) and False (F)).
2. Column for ¬p: This is the negation of p. It will be True when p is False and vice versa.
3. Column for p→q: This is True unless p is True and q is False.
4. Column for ¬p→q: This is True unless ¬p is True (which means p is False) and q is False.
5. Column for (¬p→q)→q: This is True unless (¬p→q) is True and q is False.
6. Final Column for (p→q)→((¬p→q)→q): This is True unless p→q is True and (¬p→q)→q is False.
Step 3: Analyze the Final Column
In the final column, we observe that all entries are True (T). This indicates that the expression (p→q)→((¬p→q)→q) is always true regardless of the truth values of p and q.
Conclusion
Since the final column contains only True values, we conclude that the expression is a tautology.
We will create a truth table with columns for p, q, ¬p, p→q, ¬p→q, (¬p→q)→q, and finally (p→q)→((¬p→q)→q).
|-------|-------|------------|--------------|-------------------|---------------------------|------------------------------------------|
| T | T | F | T | T | T | T |
| T | F | F | F | T | F | T |
| F | T | T | T | T | T | T |
| F | F | T | T | F | F | T |
1. Column for p and q: List all combinations of truth values for p and q (True (T) and False (F)).
2. Column for ¬p: This is the negation of p. It will be True when p is False and vice versa.
3. Column for p→q: This is True unless p is True and q is False.
4. Column for ¬p→q: This is True unless ¬p is True (which means p is False) and q is False.
5. Column for (¬p→q)→q: This is True unless (¬p→q) is True and q is False.
6. Final Column for (p→q)→((¬p→q)→q): This is True unless p→q is True and (¬p→q)→q is False.
In the final column, we observe that all entries are True (T). This indicates that the expression (p→q)→((¬p→q)→q) is always true regardless of the truth values of p and q.
Since the final column contains only True values, we conclude that the expression is a tautology.
Topper's Solved these Questions
- MODEL TEST PAPER - 17BOOK - ICSECHAPTER - MODEL TEST PAPER - 17EXERCISE - SECTION -C
10 Videos
- MODEL TEST PAPER - 17BOOK - ICSECHAPTER - MODEL TEST PAPER - 17EXERCISE - SECTION -C
10 Videos
- MODEL TEST PAPER - 10 BOOK - ICSECHAPTER - MODEL TEST PAPER - 10 EXERCISE - SECTION - C
5 Videos
- MODEL TEST PAPER - 20 BOOK - ICSECHAPTER - MODEL TEST PAPER - 20 EXERCISE - SECTION - C
10 Videos
Similar Questions
Knowledge Check
The given truth table is for which
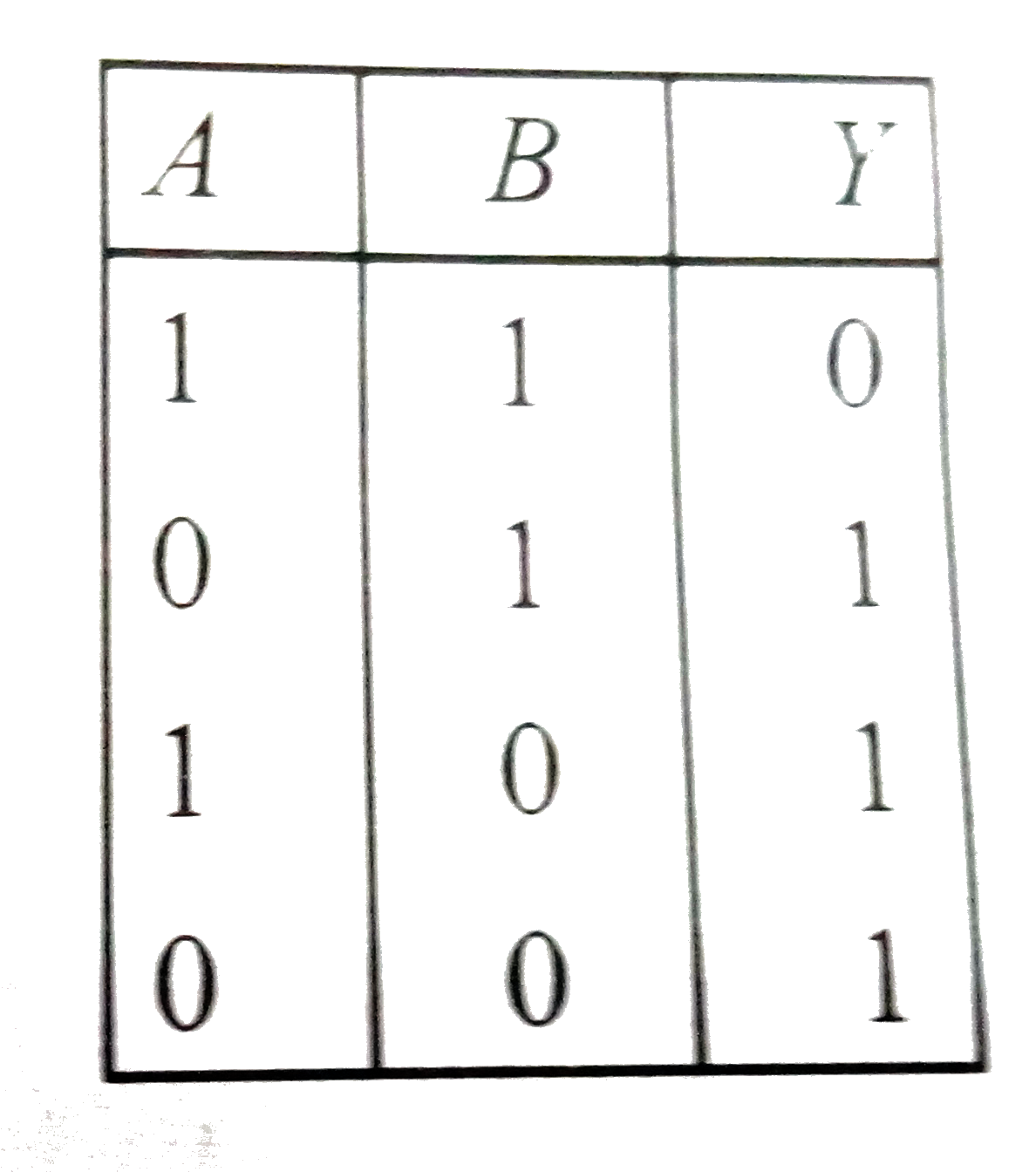 ANANDBXORCNORDOR
ANANDBXORCNORDOR
Prove by construction of truth table that p∨~(p∧q) is a tautology
View SolutionUsing truth table, prove that ~(p⇔~q) is equivalent to p⇔q.
View SolutionGiven Truth table is correct for :

View SolutionUsing truth table show that −(p∨q)∨(~p∧q) is logically equivalent to ~ p.
View SolutionGive the truth table of ~p∨q
View SolutionConsider :
Statement I:
(p∧~q)∧(~p∧q) is a fallacy
Statement II: (p→q)↔(~q→~p) is a tautology
View SolutionThe following truth table corresponds to
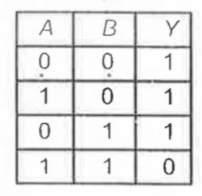
View Solution
