Determine whether p,q and "If p, then q " are true or false in each case given below :
5x3=16
The correct Answer is:pqp⇒qFFT
To determine the truth values of p, q, and "If p, then q" (denoted as p→q), we first need to define what p and q represent in the context of the statement given: 5×3=16.
Step 1: Define p and q
Let:
- p: The statement 5×3=16
- q: A statement that we can define as true or false based on the context. However, since we are only given one equation, we will consider q as a separate statement that we need to evaluate.
Step 2: Evaluate p
We evaluate p:
- 5×3=15, which is not equal to 16.
- Therefore, p is false.
Step 3: Evaluate q
Since q is not explicitly defined in the problem, we can assume it to be another statement that could be true or false. However, for the sake of this problem, we can assume q is also false because we are not given a specific statement to evaluate.
Step 4: Evaluate p→q
The implication p→q (If p, then q) is evaluated based on the truth values of p and q:
- The truth table for p→q is as follows:
- If p is true and q is true, then p→q is true.
- If p is true and q is false, then p→q is false.
- If p is false and q is true, then p→q is true.
- If p is false and q is false, then p→q is true.
Since we have established that both p and q are false:
- p is false.
- q is false.
- Therefore, p→q is true.
Summary of Truth Values
- p: False
- q: False
- p→q: True
Final Conclusion
In conclusion, for the statement 5×3=16:
- p is false.
- q is false.
- The implication p→q is true.
Let:
- p: The statement 5×3=16
- q: A statement that we can define as true or false based on the context. However, since we are only given one equation, we will consider q as a separate statement that we need to evaluate.
We evaluate p:
- 5×3=15, which is not equal to 16.
- Therefore, p is false.
Since q is not explicitly defined in the problem, we can assume it to be another statement that could be true or false. However, for the sake of this problem, we can assume q is also false because we are not given a specific statement to evaluate.
The implication p→q (If p, then q) is evaluated based on the truth values of p and q:
- The truth table for p→q is as follows:
- If p is true and q is true, then p→q is true.
- If p is true and q is false, then p→q is false.
- If p is false and q is true, then p→q is true.
- If p is false and q is false, then p→q is true.
- p is false.
- q is false.
- Therefore, p→q is true.
- p: False
- q: False
- p→q: True
In conclusion, for the statement 5×3=16:
- p is false.
- q is false.
- The implication p→q is true.
Topper's Solved these Questions
- MATHEMATICAL REASONINGBOOK - ICSECHAPTER - MATHEMATICAL REASONINGEXERCISE - EXERCISE 27 (F)
28 Videos
- MATHEMATICAL REASONINGBOOK - ICSECHAPTER - MATHEMATICAL REASONINGEXERCISE - EXERCISE 27 (G)
7 Videos
- MATHEMATICAL REASONINGBOOK - ICSECHAPTER - MATHEMATICAL REASONINGEXERCISE - EXERCISE 27 (D)
31 Videos
- MATHEMATICAL INDUCTIONBOOK - ICSECHAPTER - MATHEMATICAL INDUCTIONEXERCISE - Exercise (a)
1 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - EXERCISE
14 Videos
Similar Questions
Determine whether p,q and "If p, then q " are true or false in each case given below :
1 > 5
View SolutionDetermine whether p,q and "If p, then q " are true or false in each case given below :
3 >2
View SolutionDetermine whether p,q and "If p, then q " are true or false in each case given below :
(P) 3 is a prime number
View SolutionDetermine whether p,q and "If p, then q " are true or false in each case given below :p :
5<7, q : 5 is an odd number
View SolutionDetermine whether p,q and "If p, then q " are true or false in each case given below :
3(5÷6)<1
View SolutionState in each case, whether the given statement is true or false :
0∈ϕ
View SolutionIF p and q are in direct variation of x, y and z in the table given below:
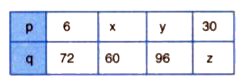
View SolutionAnswer in true or false:
p+q=q−p
View SolutionState whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.(i) If P={m,n} and Q={n,m}, then P×Q={(m,n),(n,m)}.
View SolutionIn each of the following determine whether the statement is true or false. If it is true prove it . if it is false, give an example: If x∈A and A∈B, then x∈B
View Solution
