Attempt this question on graph paper.
Write down :
the single transformation that maps A' to A''.
The correct Answer is:Reflection in y - axis
To solve the problem of finding the single transformation that maps point A' to A'', we will follow these steps:
1. Assume Point A:
Let's assume point A has coordinates (1, 2).
Hint: You can choose any point for A, but for this example, we will use (1, 2).
2. Find A':
A' is the transformation of A about the x-axis. The transformation about the x-axis changes the y-coordinate to its negative while keeping the x-coordinate the same.
- So, A' = (x, -y) = (1, -2).
Hint: Remember that reflecting a point over the x-axis means changing the sign of the y-coordinate.
3. Find A'':
A'' is the transformation of A' about the origin. The transformation about the origin changes both the x and y coordinates to their negatives.
- Therefore, A'' = (-x, -y) = (-1, 2).
Hint: Reflecting a point over the origin means changing the signs of both coordinates.
4. Determine the Transformation from A' to A'':
Now we need to find the single transformation that maps A' to A''.
- A' = (1, -2) and A'' = (-1, 2).
- The transformation that maps (1, -2) to (-1, 2) is a reflection about the line y = x.
Hint: To find the transformation, think about how the coordinates change from A' to A''.
Final Answer:
The single transformation that maps A' to A'' is a reflection about the line y = x.
Let's assume point A has coordinates (1, 2).
A' is the transformation of A about the x-axis. The transformation about the x-axis changes the y-coordinate to its negative while keeping the x-coordinate the same.
- So, A' = (x, -y) = (1, -2).
A'' is the transformation of A' about the origin. The transformation about the origin changes both the x and y coordinates to their negatives.
- Therefore, A'' = (-x, -y) = (-1, 2).
Now we need to find the single transformation that maps A' to A''.
- A' = (1, -2) and A'' = (-1, 2).
- The transformation that maps (1, -2) to (-1, 2) is a reflection about the line y = x.
The single transformation that maps A' to A'' is a reflection about the line y = x.
Similar Questions
Name a single transformation that maps P' to P''.
View SolutionAttempt this question on graph paper.
Write down :
the measure of angle ABB'
View SolutionAttempt this question on graph paper.
Write down :
the geometrical name of the figure ABB'A'
View SolutionAttempt this question on graph paper.
Write down :
the image A'' of A . When A is reflected in the origin.
View SolutionThe point A(4, 6) is first reflected in the origin to point A'. Point A' is then reflected in the y-axis to point A".
Write down a single transformation that maps A onto A"
View SolutionThe point A(-3, 2) is reflected in the x-axis to the point A'. Point A' is then reflected in the origin to point A".
Write down a single transformation that maps A onto A".
View SolutionWrite the energy transformation in Battery .
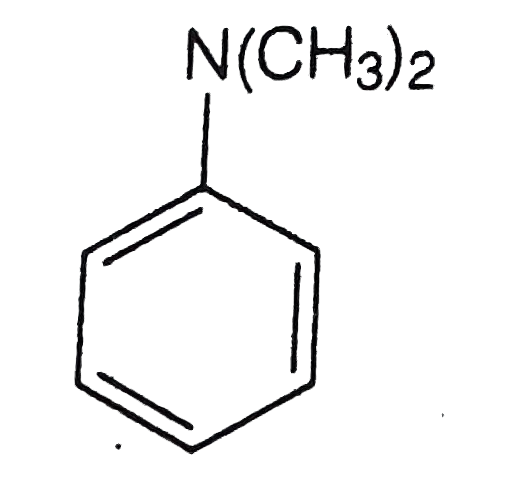
View SolutionWrite down the IUPAC name of
View SolutionThe triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C''.
Write down a single transformation that maps triangle ABC onto triangle A"B"C".
View SolutionWrite the energy transformation in Washing machine.
View Solution
