Rohit borrows Rs 86,000 from Arun for two years at 5% per annum simple interest. He immediately lends out this money to Akshay at 5% compound interest compounded annually for the same period. Calculate Rohit's profit in the transaction at the end of two years.
The correct Answer is:Rs 215
To solve the problem step-by-step, we will calculate the simple interest Rohit has to pay to Arun and the compound interest he earns from Akshay. Finally, we will find Rohit's profit from the transaction.
Step 1: Calculate the Simple Interest Rohit has to pay to Arun
The formula for Simple Interest (SI) is:
SI=P×R×T100
Where:
- P=86000 (Principal amount borrowed)
- R=5% (Rate of interest)
- T=2 years (Time period)
Substituting the values into the formula:
SI=86000×5×2100
Calculating the values:
SI=86000×10100=860000100=8600
Step 2: Calculate the Compound Interest Rohit earns from Akshay
The formula for the Amount (A) in Compound Interest is:
A=P(1+R100)T
Where:
- P=86000 (Principal amount lent)
- R=5% (Rate of interest)
- T=2 years (Time period)
Substituting the values into the formula:
A=86000(1+5100)2
Calculating:
A=86000(1+0.05)2=86000(1.05)2=86000×1.1025
Calculating the amount:
A=86000×1.1025=94815
Step 3: Calculate the Compound Interest earned
The Compound Interest (CI) is given by:
CI=A−P
Substituting the values:
CI=94815−86000=8815
Step 4: Calculate Rohit's Profit
Rohit's profit is the difference between the compound interest earned and the simple interest paid:
Profit=CI−SI
Substituting the values:
Profit=8815−8600=215
Final Answer
Rohit's profit in the transaction at the end of two years is Rs 215.
---
The formula for Simple Interest (SI) is:
SI=P×R×T100
Where:
- P=86000 (Principal amount borrowed)
- R=5% (Rate of interest)
- T=2 years (Time period)
SI=86000×5×2100
Calculating the values:
SI=86000×10100=860000100=8600
The formula for the Amount (A) in Compound Interest is:
A=P(1+R100)T
Where:
- P=86000 (Principal amount lent)
- R=5% (Rate of interest)
- T=2 years (Time period)
A=86000(1+5100)2
Calculating:
A=86000(1+0.05)2=86000(1.05)2=86000×1.1025
Calculating the amount:
A=86000×1.1025=94815
The Compound Interest (CI) is given by:
CI=A−P
Substituting the values:
CI=94815−86000=8815
Rohit's profit is the difference between the compound interest earned and the simple interest paid:
Profit=CI−SI
Substituting the values:
Profit=8815−8600=215
Rohit's profit in the transaction at the end of two years is Rs 215.
Topper's Solved these Questions
- COMPOUND INTEREST (USING FORMULA)BOOK - ICSECHAPTER - COMPOUND INTEREST (USING FORMULA)EXERCISE - EXERCISE 3(D)
22 Videos
- COMPOUND INTEREST BOOK - ICSECHAPTER - COMPOUND INTEREST EXERCISE - TOPIC 2 (4 Marks Questions)
12 Videos
- CONSTRUCTION OF POLYGONSBOOK - ICSECHAPTER - CONSTRUCTION OF POLYGONSEXERCISE - Exercise 15
76 Videos
Similar Questions
Mohan borrowed Rs. 16,000 for 3 years at 5% per annum compound interest. Calculate the amount that Mohan would have to pay at the end of 3 years.
View SolutionMawa Lal borrowed Rs 20000 from his friend Rooplal at 18% per annum simple interest . He lent it to Rampal at the same rate but compounded annually. Find his gain after 2 years.
View SolutionRekha borrowed Rs. 40,000 for 3 years at 10% per annum compound interest. Calculate the interest paid by her for the second year.
View Solution16,000 is invested at 5% compound interest compounded per annum. Use the table, given below, to find the amount in 4 years.
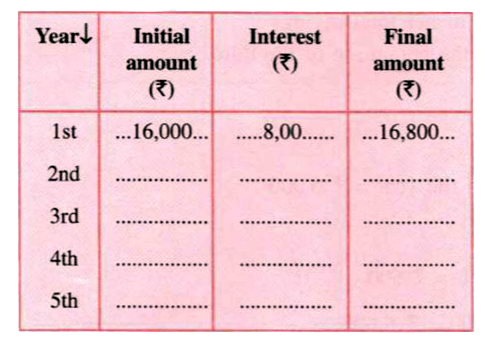
View SolutionA man borrowed Rs. 20,000 for 2 years at 8% per year compound interest. Calculate :
the interest of the second year.
View SolutionA man borrowed Rs. 20,000 for 2 years at 8% per year compound interest. Calculate :
the interest of the first year.
View SolutionA sum of Rs. 8,000 is invested for 2 years at 10% per annum compound interest. Calculate :
interest for the first year.
View SolutionA sum of Rs. 8,000 is invested for 2 years at 10% per annum compound interest. Calculate :
interest for the second year.
View SolutionA man borrowed Rs. 20,000 for 2 years at 8% per year compound interest. Calculate :
the compound interest of two years.
View SolutionA sum of Rs. 8,000 is invested for 2 years at 10% per annum compound interest. Calculate :
final amount at the end of the second year.
View Solution
