A bulb of unknown volume V contains an ideal gas at 1 atm pressure. This bulb was connected to another evacuated bulb of volume 0.5 litre through a stopcock. When the stopcock was opened the pressure at each became 530 mm while the temperature remained constant. Find V in litres.
To solve the problem, we will use the ideal gas law and the principle of conservation of moles. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
We have a bulb of unknown volume V containing an ideal gas at a pressure of 1 atm. This is our initial state.
Step 2: Convert Initial Pressure to mmHg
Since the final pressure is given in mmHg, we need to convert the initial pressure from atm to mmHg.
1 atm = 760 mmHg, so:
P1=1 atm=760 mmHg
Step 3: Identify the Final Conditions
When the stopcock is opened, the pressure in both bulbs becomes 530 mmHg. The second bulb has a volume of 0.5 L.
Step 4: Apply the Ideal Gas Law
Using the ideal gas law, we can set up the equation based on the initial and final states. The equation we will use is:
P1V1=P2V2
Where:
- P1=760 mmHg
- V1=V (unknown volume of the first bulb)
- P2=530 mmHg
- V2=V+0.5 L (total volume after opening the stopcock)
Step 5: Set Up the Equation
Substituting the known values into the equation:
760 mmHg⋅V=530 mmHg⋅(V+0.5)
Step 6: Expand and Rearrange the Equation
Expanding the right side gives:
760V=530V+265
Now, rearranging the equation to isolate V:
760V−530V=265
230V=265
Step 7: Solve for V
Now, divide both sides by 230 to find V:
V=265230≈1.15 L
Step 8: Final Result
Thus, the volume V of the bulb is approximately:
V≈1.15 L
We have a bulb of unknown volume V containing an ideal gas at a pressure of 1 atm. This is our initial state.
Since the final pressure is given in mmHg, we need to convert the initial pressure from atm to mmHg.
1 atm = 760 mmHg, so:
P1=1 atm=760 mmHg
When the stopcock is opened, the pressure in both bulbs becomes 530 mmHg. The second bulb has a volume of 0.5 L.
Using the ideal gas law, we can set up the equation based on the initial and final states. The equation we will use is:
P1V1=P2V2
Where:
- P1=760 mmHg
- V1=V (unknown volume of the first bulb)
- P2=530 mmHg
- V2=V+0.5 L (total volume after opening the stopcock)
Substituting the known values into the equation:
760 mmHg⋅V=530 mmHg⋅(V+0.5)
Expanding the right side gives:
760V=530V+265
Now, rearranging the equation to isolate V:
760V−530V=265
230V=265
Now, divide both sides by 230 to find V:
V=265230≈1.15 L
Thus, the volume V of the bulb is approximately:
V≈1.15 L
Topper's Solved these Questions
- PROPERTIES OF GASESBook:RC MUKHERJEEChapter:PROPERTIES OF GASESExercise:PROBLEMS
Explore 41 Videos
- PROPERTIES OF GASESBook:RC MUKHERJEEChapter:PROPERTIES OF GASESExercise:OBJECTIVE PROBLEMS
Explore 5 Videos
- PROBLEMS BASED ON EQUATIONS: STOICHIOMETRY Book:RC MUKHERJEEChapter:PROBLEMS BASED ON EQUATIONS: STOICHIOMETRY Exercise:OBJECTIVE PROBLEMS
Explore 15 Videos
- SOLID AND LIQUID STATES Book:RC MUKHERJEEChapter:SOLID AND LIQUID STATES Exercise:OBJECTIVE PROBLEMS
Explore 51 Videos
Similar Questions
A bulb of unknown volume V contains a gas at 1 atm pressure. This bulb was connected to another evacuated bulb of volume 0.5 L through a stop cock. When the stop cock was opened, the pressure at each bulb becomes 7.58×104Pa mm while the temperature remained constant. Calculate V in litres.
View SolutionA bulb 'X' of unknown volume containing a gas at one atmospheric pressure is connected to an evacuated bulb of 0.5 litre capacity through a stop -cock. On opening the stop-cock, the pressure in the whole system after some time was found to have a constant value of 570 mm at the same temperature. What is the volume of the bulb X ?
View Solution
Knowledge Check
A vessel containing 9 litres of an ideal gas at 760mm pressure is connected to an evacuated 9 litre vessel. The resultant pressure is
A380mmB760mmC190mmD1140mmA vessel containing 5 litres of a gas at 0.8 m pressure is connected to an evacuated vessel of volume 3 litres. The resultant pressure inside with be (assuming whole system to be isolated)
A43mB0.5mC2.0mD34mA sample of gas at room temperature is placed in an evacuated bulb of volume 0.51L and is found to exert a pressure of 24kPa. This bulb is connected to another evacuated bulb whose volume is 0.63L, and the gas is allowed to fill both bulbs. What is the new pressure of the gas at room temperature ?
A9kPaB11kPaC7kPaD5kPa
A bulb A containing gas at 1.5 bar pressure was connected to an evacuated vessel of 1.0 dm3 capacity through a stopcock. The final pressure of the system dropped to 920 mbar at the same temperature. What is the volume of the container A?
View SolutionA vessel A of volume 5 litre has a gas at pressure of 80 cm column of Hg. This is joined to another evacuated vessel B of volume 3 litre. If now the stopcock S is opened and the apprature is maintained at constant temperature then the common pressure will become -
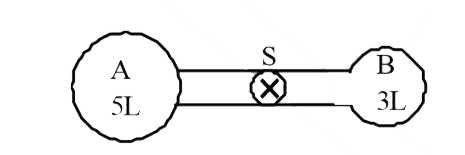
View SolutionA 8 litre container has gas at 14 atm. Container is connected to another empty vessel of volume 20 litres. Find the pressure exerted by the gas in the new system at constant temperature.
View SolutionA bulb of unknown volume contained an ideal gas at 650 mm pressure. A certain amount of gas was withdraw and found to occupy 1.52 cc at 1 atm pressure. The pressure of the gas remaining in the bulb was 600 mm. If all measurements were made at a constant temperature, find the volume of the bulb.
View SolutionThe stop cock containing two bulbs of volume 5 litre and 10 litre containing an ideal gas-at 9 atm and 6 atm respectively is opened. What is the final pressure in atm if the temperature remains the same ?
View Solution

