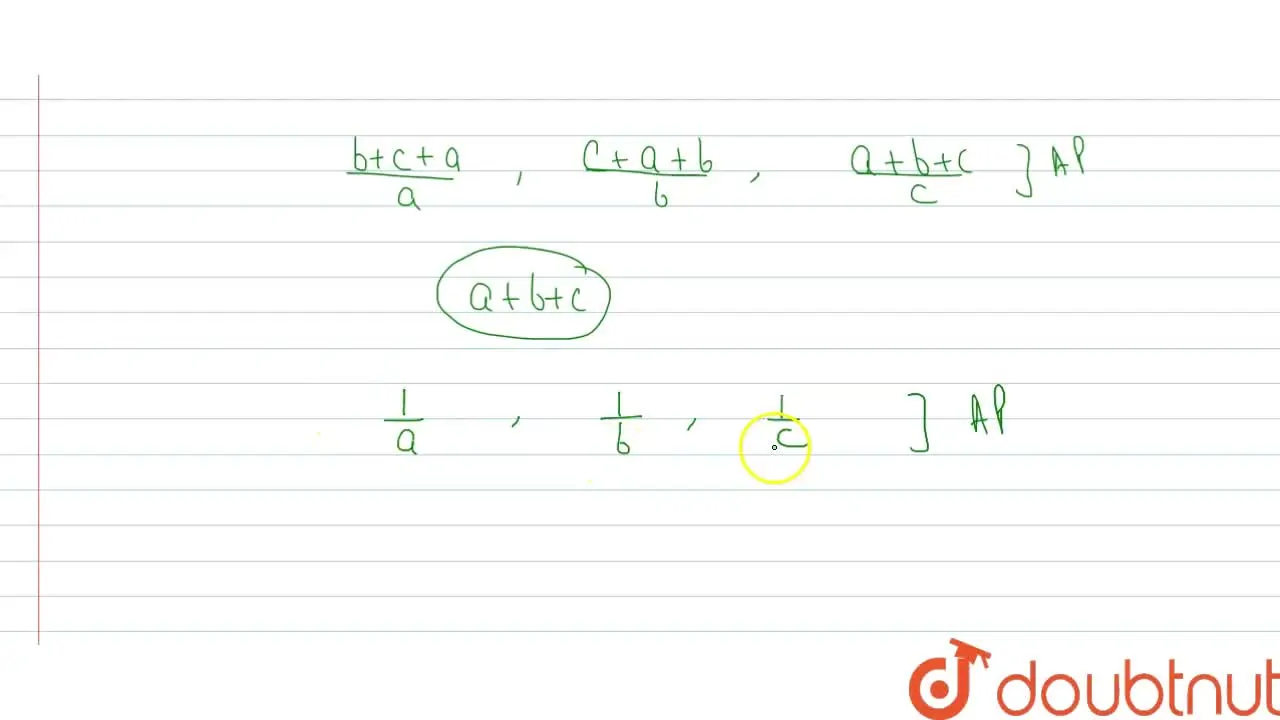
If b+c−aa,c+a−bb,a+b−cc are in A.P. then prove that 1a,1b,1c are also in A.P.
Step by step video & image solution for If (b+c-a)/(a) , (c+a-b)/(b) , (a+b-c)/(c) are in A.P. then prove that (1)/(a),(1)/(b),(1)/(c) are also in A.P. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - ICSECHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE 14 (e)17videos
SEQUENCE AND SERIES
- BOOK - ICSECHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE 14 (f)31videos
SEQUENCE AND SERIES
- BOOK - ICSECHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE 14 (c)32videos
SEQUENCE AND SERIES
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - SECTION C11videos
SELF ASSESSMENT PAPER 5
- BOOK - ICSECHAPTER - SEQUENCES AND SERIESEXERCISE - MULTIPLE CHOICE QUESTIONS34videos
SEQUENCES AND SERIES
Similar Questions
If a(b+c),b(c+a),c(a+b) are in A.P. , prove that 1a,ab,1c are also ln A.P.
View SolutionIf 1a,1b,1c are also in A.P. then prove that : (i) (b+c)a,(c+a)b,(a+b)c are also in A.P. (ii) (b+c−a)a,(c+a−b)b,(a+b−c)c are also in A.P.
View SolutionIf b+c−2aa,c+a−2bb,a+b−2cc are in A.P. , then a,b,c are in :
View SolutionIf b+c−aa,c+a−bb,a+b−cc, are in A.P., prove that 1a,1b,1c are also in A.P.
View SolutionIf (b−c)2,(c−a)2,(a−b)2 are in A.P., then prove that 1b−c,1c−a,1a−b are also in A.P.
View SolutionIf (b−c)2,(c−a)2,(a−b)2 are in A.P., then prove that 1b−c,1c−a,1a−b are also in A.P.
View SolutionIf (b−c)2,(c−a)2,(a−b)2 are in A.P., then prove that 1b−c,1c−a,1a−b are also in A.P.
View SolutionIf (b+c)−1,(c+a)−1,(a+b)−1 are in A.P. then show that ab+c,bc+a,ca+b are also in A.P.
View SolutionIf a2,b2,c2 are in A.P., prove that 1b+c,1c+a,1a+b are also in A.P.
View SolutionIf b+c−aa,b+c−ab,b+c−ac, are in A.P., prove that 1a,1b,1c are also in A.P.
View Solution