Find the value of :
10C4
The correct Answer is:210
To find the value of (104), we will use the formula for combinations:
(nr)=n!r!(n−r)!
In this case, n=10 and r=4. Therefore, we can substitute these values into the formula:
(104)=10!4!(10−4)!=10!4!⋅6!
Next, we can express 10! in a way that allows us to cancel 6!:
10!=10×9×8×7×6!
Now substituting this back into our equation gives:
(104)=10×9×8×7×6!4!⋅6!
We can cancel 6! from the numerator and the denominator:
(104)=10×9×8×74!
Next, we need to calculate 4!:
4!=4×3×2×1=24
Now we can substitute this value back into our equation:
(104)=10×9×8×724
Calculating the numerator:
10×9=90
90×8=720
720×7=5040
Now we have:
(104)=504024
Finally, we perform the division:
504024=210
Thus, the value of (104) is:
210
90×8=720
720×7=5040
Similar Questions
If nC10=nC13 , then find the value of nC2
View SolutionFind the value of 47C4+5∑r=152−rC3
View SolutionFind the value of :
10% of 250
View Solutionlog2a=3,log3b=2,log4c=1
Find the value of 3a + 2b - 10c
View SolutionFind the values of A,B and C
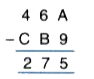
View SolutionFind the value of 5C3+4C2
View SolutionFind the value of 4C1−2C2
View SolutionFind the value of ^4nC0+4nC4+4nC8++4nC4n .
View SolutionFind the value of (.10C10)+(.10C0+.10C1)+(.10C0+.10C1+.10C2)+....+(.10C0+.10C1+.10C2+.....+.10C9).
View SolutionIf nC10=nC14, find the value of nC20and25Cn.
View Solution

