A crowbar 2 m long is pivoted about a point 10 cm from its tip.
(i) Calculate the mechanical advantage of the crowbar.
(ii) What is the least force which must be applied at the other end to displace a load of 100 kgf?
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Understand the setup
We have a crowbar that is 2 meters long, and it is pivoted 10 cm (0.1 m) from its tip. This means the distance from the pivot to the load (load arm) and the distance from the pivot to where the effort is applied (effort arm) needs to be calculated.
Step 2: Calculate the load arm
The load arm is the distance from the pivot to the point where the load is applied. Since the crowbar is 2 m long and the pivot is 0.1 m from the tip, the load arm can be calculated as:
Load arm=Total length of crowbar−Distance from pivot to tip
Load arm=2m−0.1m=1.9m
Step 3: Calculate the effort arm
The effort arm is the distance from the pivot to the point where the effort is applied. Since the pivot is 0.1 m from the tip, the effort arm is:
Effort arm=Distance from pivot to the other end=2m−0.1m=1.9m
Step 4: Calculate the mechanical advantage (MA)
Mechanical advantage is defined as the ratio of the effort arm to the load arm. Thus, we can calculate MA as follows:
MA=Effort armLoad arm=1.9m0.1m=19
Step 5: Calculate the least force required to displace a load of 100 kgf
The mechanical advantage can also be expressed as:
MA=LoadEffort
Rearranging this gives:
Effort=LoadMA
Given that the load is 100 kgf, we can substitute this into the equation:
Effort=100kgf19≈5.26kgf
Final Answers
(i) The mechanical advantage of the crowbar is 19.
(ii) The least force which must be applied at the other end to displace a load of 100 kgf is approximately 5.26 kgf.
We have a crowbar that is 2 meters long, and it is pivoted 10 cm (0.1 m) from its tip. This means the distance from the pivot to the load (load arm) and the distance from the pivot to where the effort is applied (effort arm) needs to be calculated.
The load arm is the distance from the pivot to the point where the load is applied. Since the crowbar is 2 m long and the pivot is 0.1 m from the tip, the load arm can be calculated as:
Load arm=Total length of crowbar−Distance from pivot to tip
Load arm=2m−0.1m=1.9m
The effort arm is the distance from the pivot to the point where the effort is applied. Since the pivot is 0.1 m from the tip, the effort arm is:
Effort arm=Distance from pivot to the other end=2m−0.1m=1.9m
Mechanical advantage is defined as the ratio of the effort arm to the load arm. Thus, we can calculate MA as follows:
MA=Effort armLoad arm=1.9m0.1m=19
The mechanical advantage can also be expressed as:
MA=LoadEffort
Rearranging this gives:
Effort=LoadMA
Given that the load is 100 kgf, we can substitute this into the equation:
Effort=100kgf19≈5.26kgf
(i) The mechanical advantage of the crowbar is 19.
(ii) The least force which must be applied at the other end to displace a load of 100 kgf is approximately 5.26 kgf.
Topper's Solved these Questions
- MACHINESBook:ICSEChapter:MACHINESExercise:EXERCISE-3(A)
Explore 40 Videos
- MACHINESBook:ICSEChapter:MACHINESExercise:EXERCISE-3(A) MULTIPLE CHOICE TYPE
Explore 5 Videos
- HOUSEHOLD CIRCUITS Book:ICSEChapter:HOUSEHOLD CIRCUITS Exercise:EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
Explore 2 Videos
- QUESTION PAPER 2022 TERM 1Book:ICSEChapter:QUESTION PAPER 2022 TERM 1Exercise:MULTIPLE CHOICE QUESTIONS
Explore 40 Videos
Similar Questions
A crowbar of length 120 cm has its fulcrum situated at a distance of 20 cm from the load. Calculate the mechanical advantage of the crowbar.
View SolutionA body is pivoted at a point. A force of 10N is applied at a distance of 30cm from the pivot. Calculate the moment of force about the pivot.
View SolutionA pair of scissors is used to cut a piece of cloth by keeping it at a distance of 8.0 cm from its rivet and applying an effort of 10 kgf by fingers at a distance of 2.0 cm from the rivet.
(a) Find : (i) the mechanical advantage of the scissors, and (ii) the load offered by the cloth.
(b) How does the pair of scissors atc : as a force multiplier or as a speed multiplier ?
View Solution(a) (i) State the principle of moments as applied to the lever shown in Figure. And
(ii) calculate its mechanical advantage if
AB=2⋅0mandFA=20cm.
(b) Calculate the effort needed to lift and load.
View SolutionA lever of length 9 cm has its load arm 5 cm long and the effort arm is 9 cm long. (a) to which class does it belong ?
(b) Draw a diagram of the lever showing the position of the fulcrum F and directions of both the load L and effort E. (c) what is the mechanical advantage and velocity ratio if the efficiency is 100%?
(d) What will be the mechanical advantage and velocity ratio if the efficiency becomes 50%?
View SolutionThe adjacent Figure shows a fixed pulley used by a boy to lift a load of 400 N through a vertical height of 5 m in 10 s. the effort applied by the boy on the other end of the rope is 480 N.
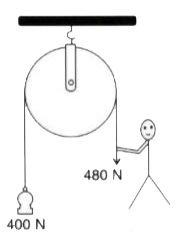
(a) What is the velocity ratio of the pulley ?
(b) What is the mechanical advantage ?
(c) Calculate the efficiency of the pully.
(d) Why is the efficiency of the pulley not 100% ?
(e) What is the energy gained by the load in 10 s?
(f) How much power was developed by the boy in raising the load ?
(g) The boy has to apply an effort which is greater than the load he is lifting. what is the justification for using the pulley ?
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

View SolutionA rod is pivoted about its centre. A 10 N force is applied 4 m from the pivot and another force of 5 N is applied 2 m from the pivot, as shown. The magnitude of the total torque about the pivot is

View SolutionA fire tongs has its arms 20 cm long. It is used to lift a coal of weight 1.5 kgf by applying an effort at a distance of 15 cm from the fulcrum. Find : (i) the mechanical advantage of the togns, and (ii) the effort needed.
View SolutionThe mass of a 10 m long wire is 100 grams. If a tension of 100 N is applied, calculate the time taken by a transverse wave to travel from one end to the other end of the wire.
View Solution

