A body ,when acted upon by a force of 10 khf , get displaced by 0.5 m.Calculate the work done by the force,when the displacement is (i) in the direction of force ,(ii)at an angle 60∘ with the force ,and (iii)normal to the force ,(g=10 N kg−1)
To solve the problem, we need to calculate the work done by a force of 10 kgf when the displacement is given in three different scenarios. Let's go through each part step by step.
Given Data:
- Force (F) = 10 kgf
- Displacement (s) = 0.5 m
- Acceleration due to gravity (g) = 10 N/kg
Step 1: Convert the Force from kgf to Newtons
1. The force in Newtons can be calculated using the formula:
F=mass×g
Here, mass is 10 kgf, which needs to be converted to Newtons:
F=10kgf×10N/kg=100N
Step 2: Calculate Work Done in Each Scenario
The formula for work done (W) is given by:
W=F⋅s⋅cos(θ)
where θ is the angle between the force and the displacement.
Part (i): Displacement in the Direction of Force
- Here, θ=0∘.
- Therefore, cos(0∘)=1.
- Now, substituting the values:
W=100N×0.5m×1=50J
Part (ii): Displacement at an Angle of 60 Degrees with the Force
- Here, θ=60∘.
- Therefore, cos(60∘)=12.
- Now, substituting the values:
W=100N×0.5m×12=25J
Part (iii): Displacement Normal to the Force
- Here, θ=90∘.
- Therefore, cos(90∘)=0.
- Now, substituting the values:
W=100N×0.5m×0=0J
Final Answers:
1. Work done when displacement is in the direction of force: 50 J
2. Work done when displacement is at an angle of 60 degrees with the force: 25 J
3. Work done when displacement is normal to the force: 0 J
- Force (F) = 10 kgf
- Displacement (s) = 0.5 m
- Acceleration due to gravity (g) = 10 N/kg
1. The force in Newtons can be calculated using the formula:
F=mass×g
Here, mass is 10 kgf, which needs to be converted to Newtons:
F=10kgf×10N/kg=100N
The formula for work done (W) is given by:
W=F⋅s⋅cos(θ)
where θ is the angle between the force and the displacement.
- Here, θ=0∘.
- Therefore, cos(0∘)=1.
- Now, substituting the values:
W=100N×0.5m×1=50J
- Here, θ=60∘.
- Therefore, cos(60∘)=12.
- Now, substituting the values:
W=100N×0.5m×12=25J
- Here, θ=90∘.
- Therefore, cos(90∘)=0.
- Now, substituting the values:
W=100N×0.5m×0=0J
1. Work done when displacement is in the direction of force: 50 J
2. Work done when displacement is at an angle of 60 degrees with the force: 25 J
3. Work done when displacement is normal to the force: 0 J
Topper's Solved these Questions
- WORK ENERGY AND POWERBook:ICSEChapter: WORK ENERGY AND POWERExercise:EXERCISE-2(B)
Explore 30 Videos
- WORK ENERGY AND POWERBook:ICSEChapter: WORK ENERGY AND POWERExercise:EXERCISE-2(B) (MULTIPLE CHOICE TYPE )
Explore 2 Videos
- WORK ENERGY AND POWERBook:ICSEChapter: WORK ENERGY AND POWERExercise:EXERCISE-2(A) (MULTIPLE CHOICE TYPE )
Explore 2 Videos
- CALORIMETRYBook:ICSEChapter:CALORIMETRYExercise:EXERCISE-11(B) (NUMERICALS)
Explore 15 Videos
Similar Questions
How is work done by a force measured when the force :
is in the direction of displacement.
View SolutionWhat is the work done by a force when the force is:
Normal to the displacement produced.
View SolutionThe relationship between force and position is shown in fig ( in one dimensional case). The work done in displacing a body from x=1cm to x = 5 cm is:
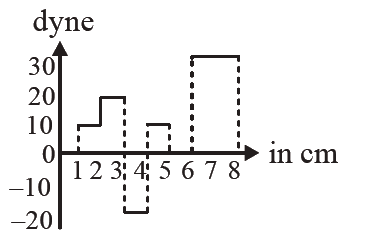
View SolutionA body, acted upon by a force of 50N, is displaced through a distance 10m in direction making an angle of 60∘ with the force. Find the work done by the force.
View SolutionHow is the work done by a force measured when (i) force is in the direction of displacement, (ii) force is at an angle to the direction of displacement ?
View SolutionFind out the work done when a force of 30 N displaces a body through 8 m in the direction of the applied force.
View Solution30 joules work is done, when a force 'F' causes a displacement of 5 m. the magnitude of force is :
View SolutionCalculate the amount of work done, when a force of 25 N displaces a body through 10 m, in its own direction.
View SolutionHow is work done by a force measured when the force :
is at an angle of displacement
View SolutionIn a force of 9 N is acting on a body, then find instataneous power supplied to the body when its velocity is 5m/s in the direction of force
View Solution

