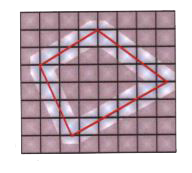
The boundary line of an irregular lamina, on a graph paper is shown in Fig. Find the approximate area of the lamina. In Fig. , the number of complete squares = 14
The number of squares more than half = 11

Total number of squares n = 14 + 11 = 25
Area of the square = 1 cm x 1 cm = 1cm2
Area of lamina = 25×1cm2=25cm2
Topper's Solved these Questions
- PHYSICAL QUANTITIES AND MEASUREMENTBook:ICSEChapter:PHYSICAL QUANTITIES AND MEASUREMENTExercise:TEST YOURSELF (TRUE OR FALSE)
Explore 9 Videos
- PHYSICAL QUANTITIES AND MEASUREMENTBook:ICSEChapter:PHYSICAL QUANTITIES AND MEASUREMENTExercise:TEST YOURSELF (FILL IN THE BLANKS)
Explore 9 Videos
- MOTIONBook:ICSEChapter:MOTIONExercise:TEST YOURSELF (NUMERICAL)
Explore 13 Videos
- SOUNDBook:ICSEChapter:SOUNDExercise:EXERCISES (PICTURE STUDY)
Explore 4 Videos
Similar Questions
Radha made a picture of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.
View SolutionFind the approximate area of an irregular lamina of which boundary line is drawn on the graph paper shown in Fig.
View SolutionFind MI of a triangular lamina of mass M about the axis of rotation AB shown in Fig.

View SolutionOn a squared paper, draw (i) a rectangle, (ii) a triangle (iii) any irregular closed figure. Find the approximate area of each by counting the number of squares complete, more than half and exactly half.
View SolutionDescribe the method in steps to find the area of an irregular lamina using a graph paper.
View SolutionA square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of square.

View SolutionFind the area of the shaded region given in Fig. 12.72, where ABCD is a square of side 14cm.
View SolutionFind the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.
View SolutionFind two positive numbers whose sum is 14 and the sum of whose squares in minimum.
View SolutionFind two positive numbers whose sum is 14 and the sum of whose squares is minimum.
View Solution

