ABCD is a gram. P and Q are two points on AB and CD such that AP : PB = 2:3 , DQ = QC = 4 : 1 Find the ratio of area of Δ DPQ and '// ABCD
The correct Answer is: ABCD
To find the ratio of the area of triangle DPQ to the area of parallelogram ABCD, we will follow these steps:
Step 1: Understand the Ratios
Given:
- AP:PB=2:3
- DQ:QC=4:1
This means that if we let AP=2x and PB=3x, then AB=AP+PB=2x+3x=5x.
Similarly, for DQ and QC, if we let DQ=4y and QC=1y, then CD=DQ+QC=4y+1y=5y.
Step 2: Area of Parallelogram ABCD
The area of the parallelogram ABCD can be calculated using the base and height. Since AB and CD are equal, we can use the length AB as the base.
Let the height from point D to line AB be h. Thus, the area of parallelogram ABCD is:
AreaABCD=Base×Height=AB×h=5x×h
Step 3: Area of Triangle DPQ
To find the area of triangle DPQ, we can use the formula for the area of a triangle:
AreaDPQ=12×Base×Height
Here, the base can be taken as PQ and the height will be the perpendicular distance from point D to line PQ.
Since DQ:QC=4:1, we can say that PQ is divided in the same ratio. The length of PQ can be calculated as follows:
- The total length of CD is 5y.
- Since DQ=4y and QC=1y, the length of PQ can be considered as PQ=DQ+AP where AP=25×AB.
Step 4: Calculate the Ratio of Areas
The area of triangle DPQ can be expressed in terms of the area of the parallelogram:
AreaDPQ=12×PQ×h′
Where h′ is the height from D to line PQ.
Since the triangles formed by the segments are similar, the ratio of the areas of triangle DPQ to parallelogram ABCD can be simplified using the ratios of their bases:
AreaDPQAreaABCD=45
Final Ratio
Thus, the ratio of the area of triangle DPQ to the area of parallelogram ABCD is:
Ratio=45
Given:
- AP:PB=2:3
- DQ:QC=4:1
The area of the parallelogram ABCD can be calculated using the base and height. Since AB and CD are equal, we can use the length AB as the base.
AreaABCD=Base×Height=AB×h=5x×h
To find the area of triangle DPQ, we can use the formula for the area of a triangle:
AreaDPQ=12×Base×Height
Here, the base can be taken as PQ and the height will be the perpendicular distance from point D to line PQ.
- The total length of CD is 5y.
- Since DQ=4y and QC=1y, the length of PQ can be considered as PQ=DQ+AP where AP=25×AB.
The area of triangle DPQ can be expressed in terms of the area of the parallelogram:
AreaDPQ=12×PQ×h′
Where h′ is the height from D to line PQ.
AreaDPQAreaABCD=45
Thus, the ratio of the area of triangle DPQ to the area of parallelogram ABCD is:
Ratio=45
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a parallelogram, P and Q are the points on the diagonal AC such that AP=QC, then quadrilateral BPDQ is a :
AtrapeziumBparallelogramCsquareDnone of theseLet AB and CD are two parallel chords of circle whose radius is 5 units. If P and Q are mid points of AB and CD respectively such that PA. PB = 9, QC. QD = 16, then distance between AB and CD is
A5B25C7D11ABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
A10 cmB5 cmC20 cmD12 cm
ABCD is a square of area 1 m2. P and Q are the midpoints of AB and BC respectively. What is the area of Δ DPQ ?
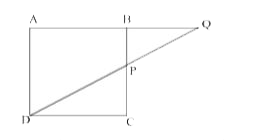
View SolutionIn the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
View SolutionABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
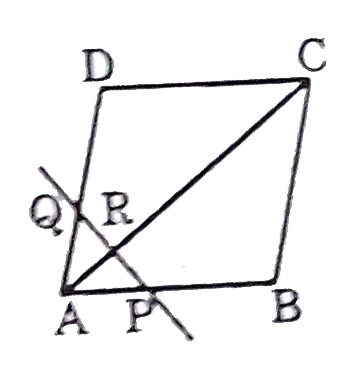
View SolutionA transversal cuts side AB and AD and diagonal AC of parallelogram ABCD in points P,Q and R respectively such that AP: PB =1 :2 and AQ: QD=2:3 . Find the ratio AR : RC
View SolutionLet AB and CD are two parallel
chords of circle whose radius is
5 units. If P and Q are mid points
of AB and CD respectively such that
P.A.PB=9,QC.QD=16,
then distance between AB and CD is
View Solution
