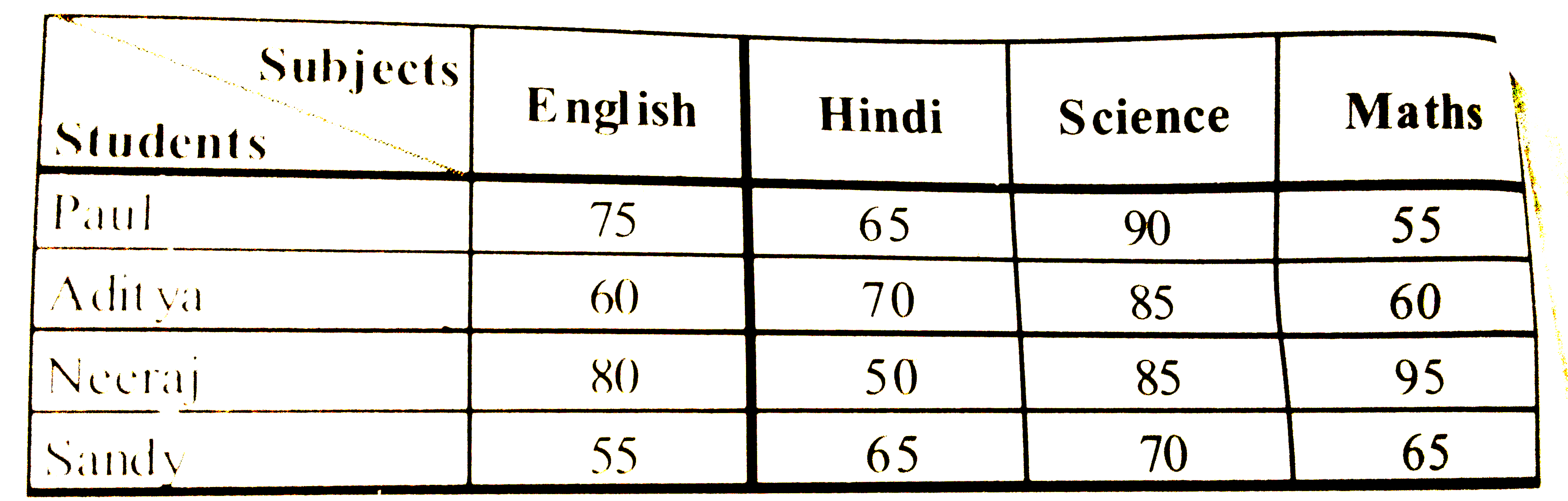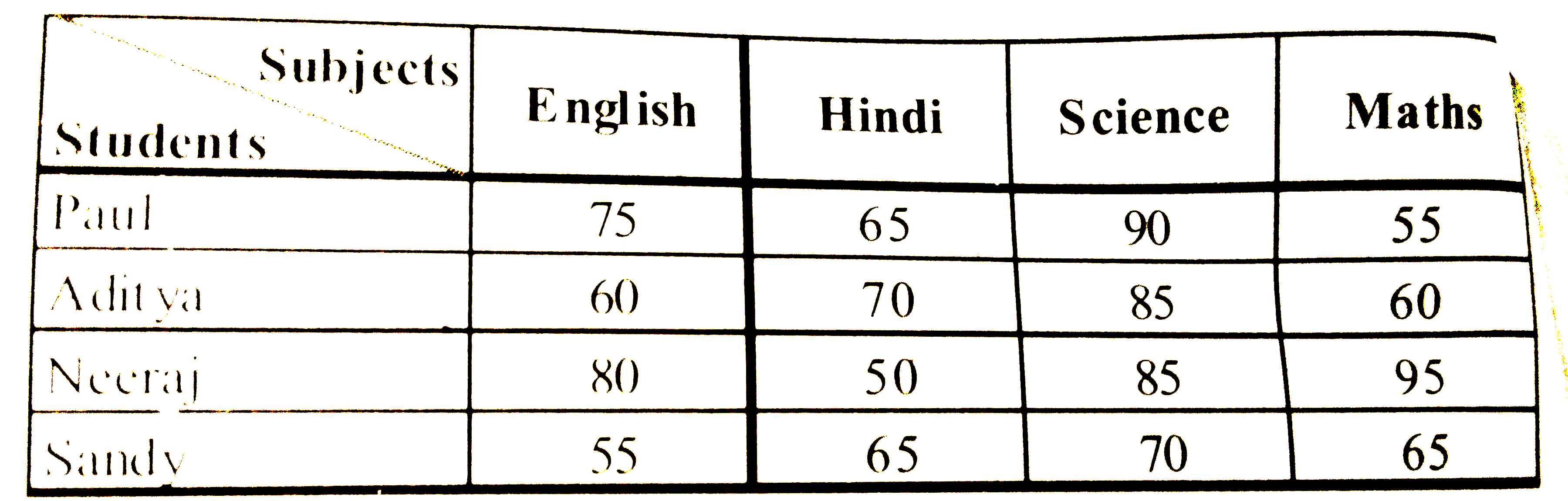The average marks scored by Ganesh in English, Science, Mathematics and History is less than 15 from that scored by him in English, History, Geography and Mathematics. What is the difference of marks in Science and Geography scored by him?
The correct Answer is:60
To solve the problem, let's denote the marks scored by Ganesh in each subject as follows:
- Let E = Marks in English
- Let S = Marks in Science
- Let M = Marks in Mathematics
- Let H = Marks in History
- Let G = Marks in Geography
According to the problem, we have two average scores:
1. The average marks in English, Science, Mathematics, and History:
Average1=E+S+M+H4
2. The average marks in English, History, Geography, and Mathematics:
Average2=E+H+G+M4
The problem states that:
Average1<Average2−15
Substituting the expressions for the averages, we get:
E+S+M+H4<E+H+G+M4−15
To eliminate the fractions, we can multiply the entire inequality by 4:
E+S+M+H<E+H+G+M−60
Now, we can simplify this inequality:
1. Cancel E, H, and M from both sides:
S<G−60
This tells us that the marks in Science (S) are less than the marks in Geography (G) minus 60.
To find the difference between the marks in Science and Geography, we can rearrange the inequality:
G−S>60
Thus, the difference between marks in Science and Geography is:
G−S=D(where D is the difference)
From the inequality, we know:
D>60
Conclusion:
The difference in marks between Science and Geography is greater than 60.
- Let S = Marks in Science
- Let M = Marks in Mathematics
- Let H = Marks in History
- Let G = Marks in Geography
Average1=E+S+M+H4
Average2=E+H+G+M4
Average1<Average2−15
E+S+M+H4<E+H+G+M4−15
E+S+M+H<E+H+G+M−60
1. Cancel E, H, and M from both sides:
S<G−60
G−S>60
G−S=D(where D is the difference)
From the inequality, we know:
D>60
The difference in marks between Science and Geography is greater than 60.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The average marks scored by Ravi in English , Science ,Mathematics and History is less than 15 from that scored by him in English , Hsitory , Geography and Mathematics .What is the difference of marks in Science and Geography secured by him ?
A40B50C60DDate inadequateRam got twice as many marks in English as in Science. His total marks in English, Science and Maths are 180. If the ratio of his marks in English and Maths is 2:3, what is his marks in Science ?
A20B60C30D40Study the following table carefully and answer the question given below
No of marks obtained by Five Students in Five Subjects in an Examination table....
What is the overall percentage marks obtained by D in History and Geography together?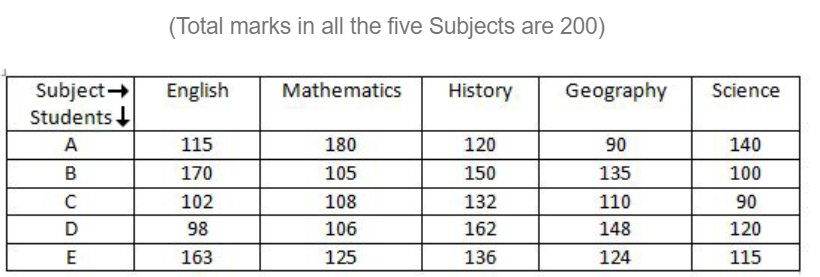 A73.40B72.80C70.50D68.80
A73.40B72.80C70.50D68.80
Shantan got 68 marks in English and 85 marks in Mathematics. Find the ratio of the marks scored in English to the Matematics.
View SolutionRam got twice as many marks in English as in Science. His total marks in English, Science and Maths are 180. If the ratio of his marks in English and Maths is 2:3, what is his marks in Science ?
View SolutionThe questions given below consists of a question followed by three statements. You have to study the question and the statements and decide which of the statement(s) is/are necessary to answer the question.
How many marks did Tarun secure in English?
I. The average marks obtained by Tarun in four subjects including English is 60.
II. The total marks obtained by him in English and Mathematics together are 170.
III. The total marks obtained by him in Mathematics and Science together are 180.
View SolutionWhat are the marks scored by Abhijit in English?
I. Marks scored by Abhijit in Mathematics are more than his marks in Science by 20
II. Total marks scored by Abhijit in Mathematics, Science and English are 197.
III. Marks scored by Abhijit in Science are more than his marks in English by 12
View SolutionWhat are the marks scored by Abhijit in English?
I. Marks scored by Abhijit in Mathematics are more than his marks in Science by 20
II. Total marks scored by Abhijit in Mathematics, Science and English are 197.
III. Marks scored by Abhijit in Science are more than his marks in English by 12
View Solution