Write the value of :
0.136 to the nearest hundredths
The correct Answer is:0.14
To round the number 0.136 to the nearest hundredths, follow these steps:
Step 1: Identify the hundredths place
The number 0.136 has three decimal places. The digit in the hundredths place is the second digit after the decimal point. In this case, the number is:
- 0.136
Here, the digit in the hundredths place is 3.
Step 2: Look at the digit in the thousandths place
Next, we need to look at the digit in the thousandths place, which is the third digit after the decimal point. In this case, the digit is:
- 0.136
Here, the digit in the thousandths place is 6.
Step 3: Apply rounding rules
According to rounding rules:
- If the digit in the thousandths place (6) is 5 or greater, we round up the digit in the hundredths place (3) by 1.
- If the digit in the thousandths place is less than 5, we keep the hundredths place digit the same.
Since 6 is greater than 5, we will round up.
Step 4: Round the number
Now, we add 1 to the digit in the hundredths place:
- 3 (hundredths place) + 1 = 4
So, we replace the hundredths place with 4.
Step 5: Write the final answer
The rounded value of 0.136 to the nearest hundredths is:
- 0.14
Summary of the steps:
1. Identify the hundredths place (3).
2. Look at the thousandths place (6).
3. Since 6 is greater than 5, round up the hundredths place from 3 to 4.
4. The final rounded value is 0.14.
---
The number 0.136 has three decimal places. The digit in the hundredths place is the second digit after the decimal point. In this case, the number is:
- 0.136
Here, the digit in the hundredths place is 3.
Next, we need to look at the digit in the thousandths place, which is the third digit after the decimal point. In this case, the digit is:
- 0.136
Here, the digit in the thousandths place is 6.
According to rounding rules:
- If the digit in the thousandths place (6) is 5 or greater, we round up the digit in the hundredths place (3) by 1.
- If the digit in the thousandths place is less than 5, we keep the hundredths place digit the same.
Now, we add 1 to the digit in the hundredths place:
- 3 (hundredths place) + 1 = 4
The rounded value of 0.136 to the nearest hundredths is:
- 0.14
1. Identify the hundredths place (3).
2. Look at the thousandths place (6).
3. Since 6 is greater than 5, round up the hundredths place from 3 to 4.
4. The final rounded value is 0.14.
Topper's Solved these Questions
- DECIMALS BOOK - ICSECHAPTER - DECIMALS EXERCISE - EXERCISE 4G
36 Videos
- DECIMALS BOOK - ICSECHAPTER - DECIMALS EXERCISE - WARM-UP EXERCISE
18 Videos
- DECIMALS BOOK - ICSECHAPTER - DECIMALS EXERCISE - EXERCISE 4E
16 Videos
- DATA HANDLING BOOK - ICSECHAPTER - DATA HANDLING EXERCISE - EXERCISE 24D
13 Videos
- EXPONENTS BOOK - ICSECHAPTER - EXPONENTS EXERCISE - EXERCISE 5
30 Videos
Similar Questions
Knowledge Check
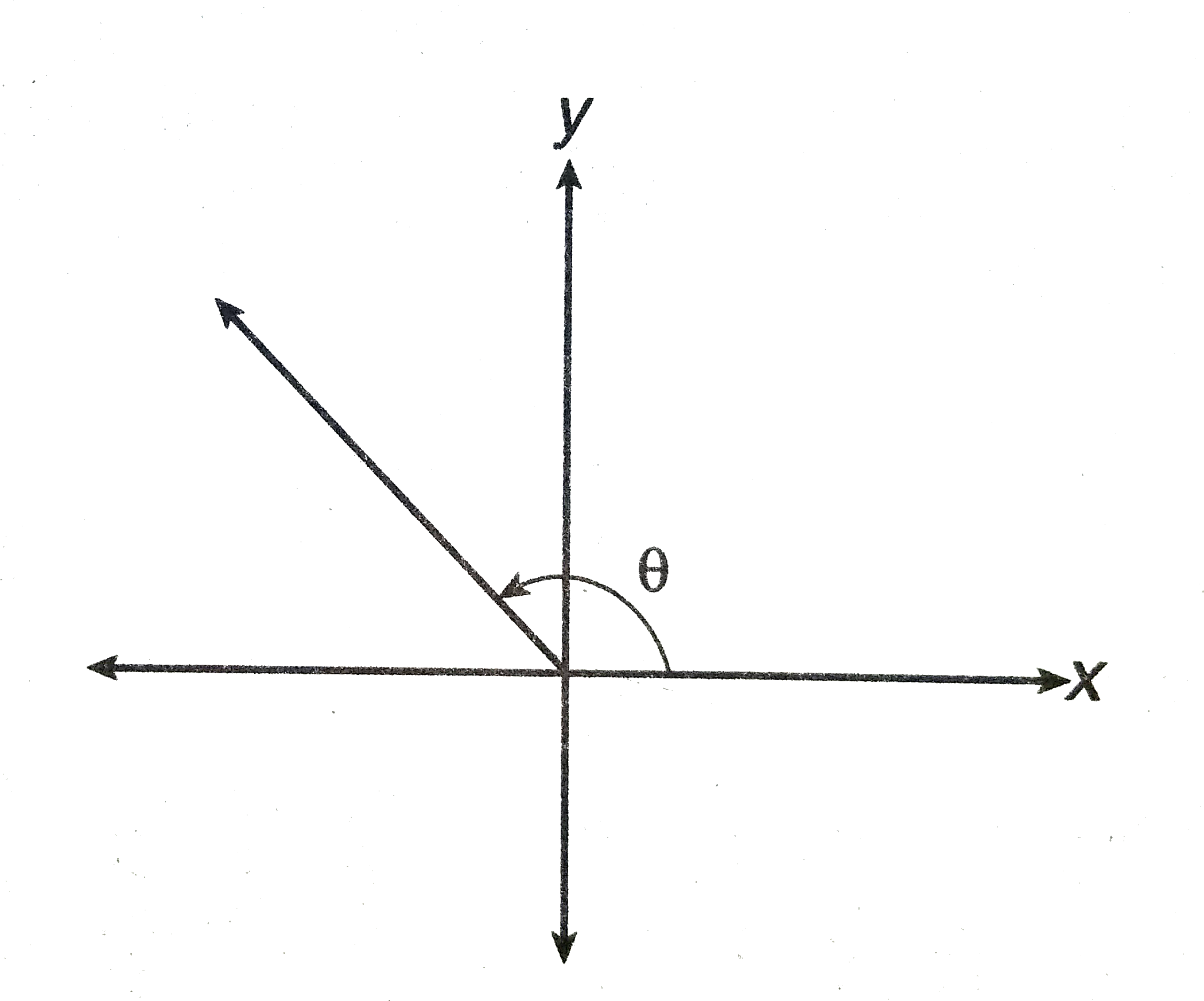
In the figure above, if cosθ=−0.36, what is the value of sinθ to the nearest hundredth?A0.64B0.80C0.93D−0.93For all numbers x[x] denotes the value of x3 rounded to the nearest multiple of ten.
Column A0<x<2Column Bx2√xAIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decideFor all numbers x[x] denotes the value of x3 rounded to the nearest multiple of ten.
Column Ax>y>0Column Bx−yx/3+y/3AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
Write the value of :
0.061 to the nearest tenths
View SolutionWrite the value of :
3.157 to the nearest tenths
View SolutionRound off :
9.837 to the nearest hundredths.
View Solution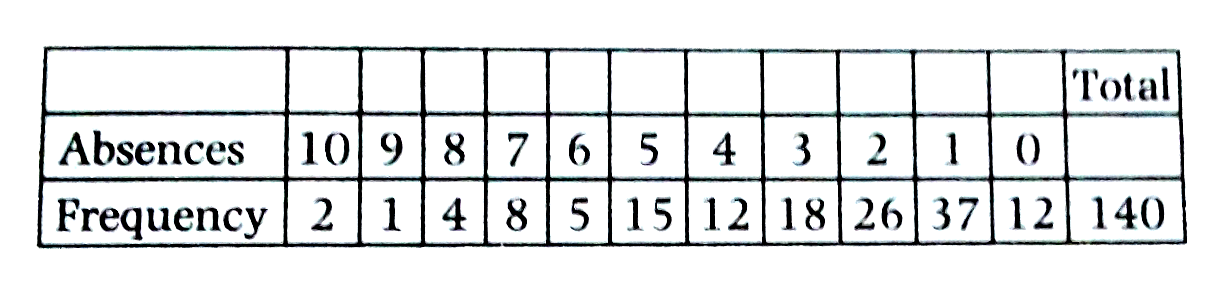
The student attendance record for a class in a one-semester course is shown above. If 2 students are chosen at random, what is the probability , to the nearest hundredth , that both students have fewer than 2 absences ?
View SolutionThe pes, a Roman measure of length, is approximately equal to 11.65 inches. It is also equivalent to 16 smaller Roman units called digits. Based on these relationships, 75 Roman digits is equivalent to how many feet––––, to the nearest hundredth? (12 inches = 1 foot)
View Solution
