A city building code requires that the area of the windows must be at least 18 of the area of the walls and roots of all new building. The daily heating cost of a new building is ₹ 3 per square meter of window area and ₹ 1 per square metre of wall and roof area. To the nearest square metre of wall and roof area. To the nearest square metre, what is the largest surface area a new building can have if its daily heating cost cannot exceed ₹ 1,000 ?
The correct Answer is:Largest surface area = 818.18aq.m≈818 sq. m (in nearest sq. m )
To solve the problem step by step, we will define the variables, set up the equations based on the given conditions, and then solve for the maximum surface area of the building.
Step 1: Define the Variables
Let:
- A = Area of the walls and roof (in square meters)
- W = Area of the windows (in square meters)
According to the problem, the area of the windows must be at least 18 of the area of the walls and roof. Therefore, we can express this relationship as:
W=A8
Step 2: Set Up the Cost Equation
The daily heating cost is given as:
- ₹ 3 per square meter for the window area
- ₹ 1 per square meter for the wall and roof area
The total heating cost C can be expressed as:
C=1⋅A+3⋅W
Substituting W from the previous step:
C=A+3⋅A8
This simplifies to:
C=A+3A8=8A8+3A8=11A8
Step 3: Set Up the Inequality
We know that the daily heating cost cannot exceed ₹ 1,000. Therefore, we set up the inequality:
11A8≤1000
Step 4: Solve for A
To isolate A, we multiply both sides of the inequality by 8:
11A≤8000
Now, divide both sides by 11:
A≤800011≈727.27
Step 5: Calculate the Maximum Window Area
Now we can calculate the maximum window area W:
W=A8≤727.278≈90.91
Step 6: Calculate the Total Surface Area
The total surface area S of the building is the sum of the wall and roof area and the window area:
S=A+W=A+A8=8A8+A8=9A8
Substituting the maximum value of A:
S≤9⋅727.278≈6545.438≈818.18
Conclusion
To the nearest square meter, the largest surface area S a new building can have is:
818 square meters
Let:
- A = Area of the walls and roof (in square meters)
- W = Area of the windows (in square meters)
W=A8
The daily heating cost is given as:
- ₹ 3 per square meter for the window area
- ₹ 1 per square meter for the wall and roof area
C=1⋅A+3⋅W
Substituting W from the previous step:
C=A+3⋅A8
This simplifies to:
C=A+3A8=8A8+3A8=11A8
We know that the daily heating cost cannot exceed ₹ 1,000. Therefore, we set up the inequality:
11A8≤1000
To isolate A, we multiply both sides of the inequality by 8:
11A≤8000
Now, divide both sides by 11:
A≤800011≈727.27
Now we can calculate the maximum window area W:
W=A8≤727.278≈90.91
The total surface area S of the building is the sum of the wall and roof area and the window area:
S=A+W=A+A8=8A8+A8=9A8
Substituting the maximum value of A:
S≤9⋅727.278≈6545.438≈818.18
To the nearest square meter, the largest surface area S a new building can have is:
818 square meters
Topper's Solved these Questions
- MODEL TEST PAPER - 8Book:ICSEChapter:MODEL TEST PAPER - 8Exercise:Section - C (In sub-parts (i) and (ii) choose the correct option and In sub-parts (iii) to (v) , answer the questions as instructed )
Explore 5 Videos
- MODEL TEST PAPER - 7Book:ICSEChapter:MODEL TEST PAPER - 7Exercise:Section - C
Explore 5 Videos
- MODEL TEST PAPER -1Book:ICSEChapter:MODEL TEST PAPER -1Exercise:Secton - C
Explore 11 Videos
Similar Questions
Knowledge Check
The perimeter of square is 36 inches . What is the area of the square , in square inches ?
A6B9C18D81The perimeter of a square plot of land is 144 metres . Find its area.
A=1286m2B=1296m2C=1276m2D=1206m2If ABCD is a square and the area of ΔAFG is 10, then what is the area of ΔAEC ?
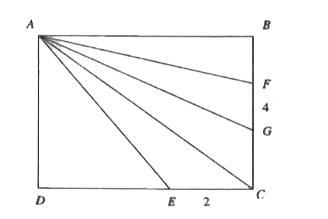 A5B10√2C10√3D10
A5B10√2C10√3D10
If the side of a square is tripled, find the new area.
View SolutionA square is of side 334 m. Find the area of the square.
View SolutionFind in square metres, the area of a square of side 16.5 dam.
View SolutionFor the adiabatic expansion of an ideal as
View SolutionWhat is the area of a square with diagonal of 6?
View Solution