Alternate interior angles between parallel lines are equal
The correct Answer is:1
Step-by-Step Solution:
1. Identify the Parallel Lines and Transversal:
- We have two parallel lines, which we will label as Line L and Line M.
- A transversal line, which we will label as Line P, intersects both parallel lines.
2. Label the Angles:
- When the transversal intersects the parallel lines, it creates four angles.
- We will label these angles as Angle 1, Angle 2, Angle 3, and Angle 4.
3. Identify Alternate Interior Angles:
- Alternate interior angles are the pairs of angles that lie between the two parallel lines but on opposite sides of the transversal.
- In this case, Angle 1 and Angle 2 are one pair of alternate interior angles, and Angle 3 and Angle 4 are another pair.
4. State the Equality of Alternate Interior Angles:
- According to the property of alternate interior angles, we can state that:
- Angle 1 = Angle 2 (since they are alternate interior angles)
- Angle 3 = Angle 4 (since they are also alternate interior angles)
5. Conclusion:
- Therefore, we conclude that alternate interior angles formed by a transversal intersecting two parallel lines are equal.
- We have two parallel lines, which we will label as Line L and Line M.
- A transversal line, which we will label as Line P, intersects both parallel lines.
- When the transversal intersects the parallel lines, it creates four angles.
- We will label these angles as Angle 1, Angle 2, Angle 3, and Angle 4.
- Alternate interior angles are the pairs of angles that lie between the two parallel lines but on opposite sides of the transversal.
- In this case, Angle 1 and Angle 2 are one pair of alternate interior angles, and Angle 3 and Angle 4 are another pair.
- According to the property of alternate interior angles, we can state that:
- Angle 1 = Angle 2 (since they are alternate interior angles)
- Angle 3 = Angle 4 (since they are also alternate interior angles)
- Therefore, we conclude that alternate interior angles formed by a transversal intersecting two parallel lines are equal.
Similar Questions
Corresponding angles between parallel lines are equal
View SolutionCo-interior angles between parallel lines are complementary angles
View SolutionSum of co-interior angles between parallel lines is two right angles
View SolutionIn the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
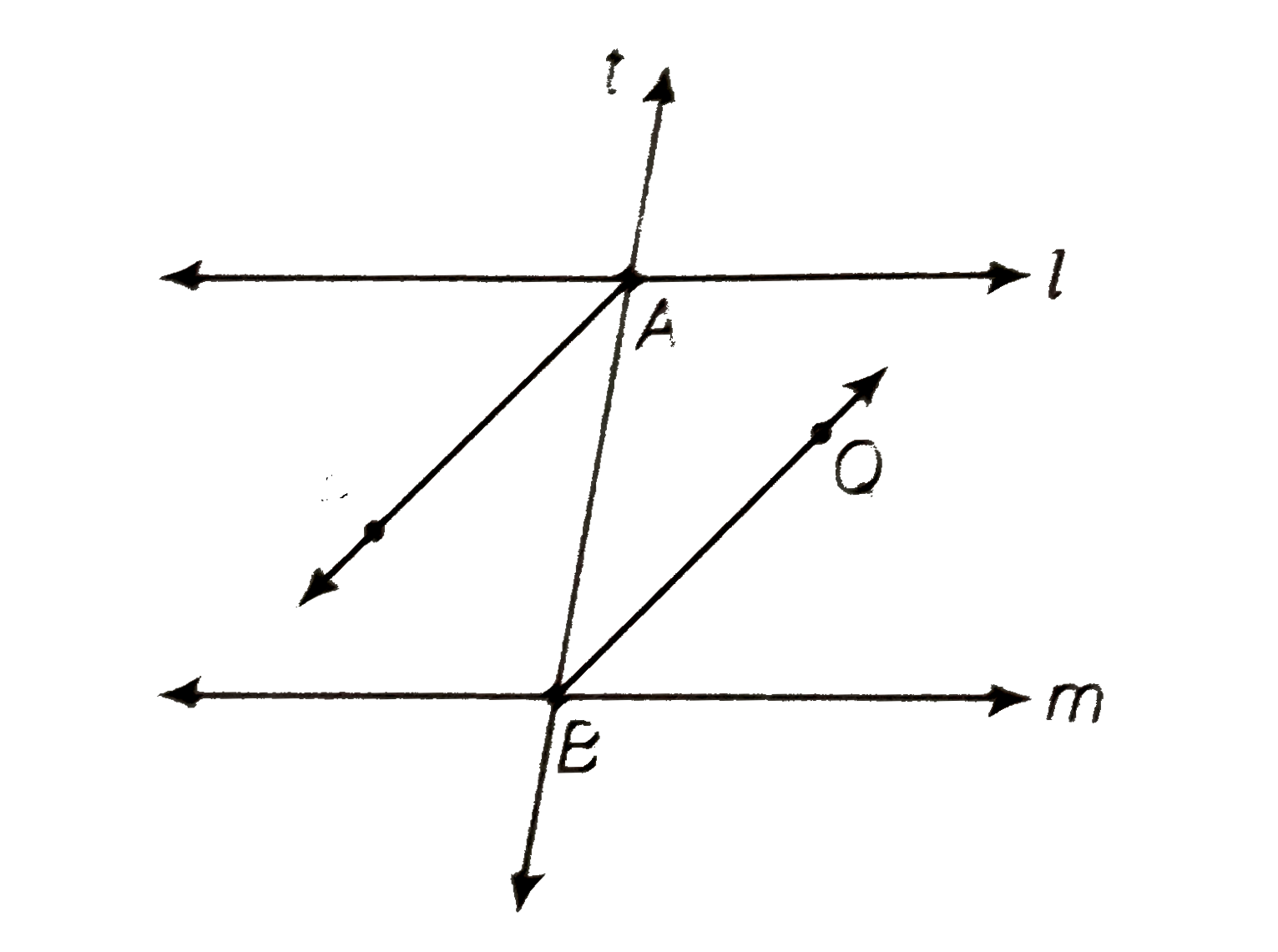
View SolutionTheorem 6.3 : If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
View SolutionIn the adjoining figure, identify(i) the pairs of corresponding angles.(ii) the pairs of alternate interior angles.(iii) the pairs of interior angles on the sameside of the transversal.(iv) the vertically opposite angles.
View SolutionIf two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3, then the measure of the larger angle is
View SolutionAngle between Lines and Planes
View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
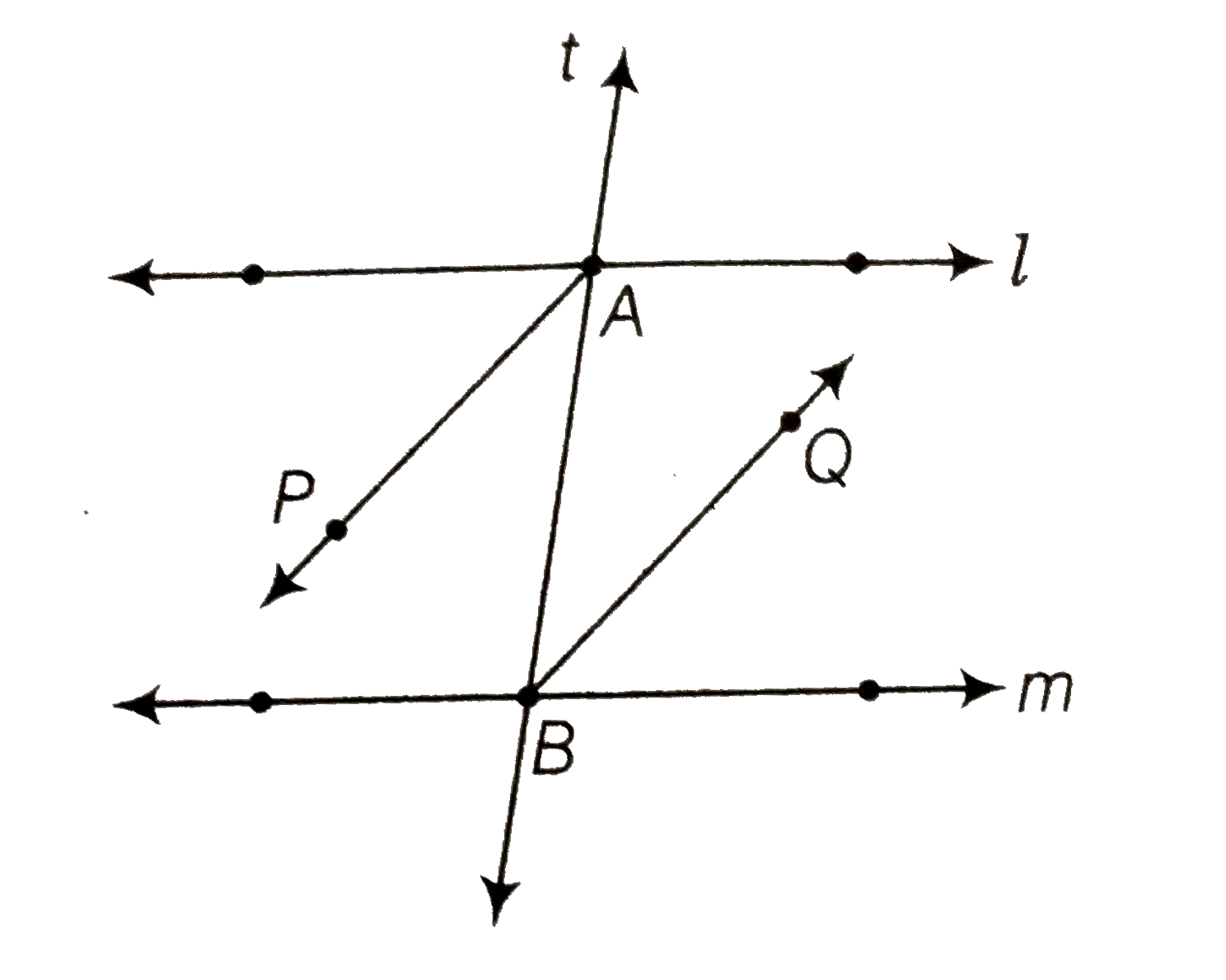
View SolutionComprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors →a,→b and →c respectively of the regular tetrahedron.
The angle between any edge and a face not containing the edge is
View Solution

