Find the reflex angle corresponding to each of the following angles:
125∘
The correct Answer is:235∘
To find the reflex angle corresponding to the angle of 125∘, we can follow these steps:
1. Understand the Definition of Reflex Angle:
A reflex angle is an angle that is greater than 180∘ but less than 360∘. It is the larger angle formed when you have a smaller angle.
2. Identify the Given Angle:
The given angle is 125∘.
3. Use the Formula for Reflex Angle:
The reflex angle can be calculated using the formula:
Reflex Angle=360∘−Given Angle
4. Substitute the Given Angle into the Formula:
Now, substitute 125∘ into the formula:
Reflex Angle=360∘−125∘
5. Perform the Calculation:
Now, subtract 125∘ from 360∘:
Reflex Angle=360∘−125∘=235∘
6. State the Final Answer:
Therefore, the reflex angle corresponding to 125∘ is 235∘.
Final Answer:
The reflex angle corresponding to 125∘ is 235∘.
A reflex angle is an angle that is greater than 180∘ but less than 360∘. It is the larger angle formed when you have a smaller angle.
The given angle is 125∘.
The reflex angle can be calculated using the formula:
Reflex Angle=360∘−Given Angle
Now, substitute 125∘ into the formula:
Reflex Angle=360∘−125∘
Now, subtract 125∘ from 360∘:
Reflex Angle=360∘−125∘=235∘
Therefore, the reflex angle corresponding to 125∘ is 235∘.
The reflex angle corresponding to 125∘ is 235∘.
Similar Questions
Knowledge Check
Name each of the following angles
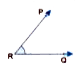 A∠QPRB∠RQPC∠RPQD∠PRQ
A∠QPRB∠RQPC∠RPQD∠PRQName each of the following angles
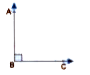 A∠BACB∠ABCC∠BCAD∠CAB
A∠BACB∠ABCC∠BCAD∠CABName each of the following angles
 A∠YXZB∠XYZC∠YZXD∠ZYX
A∠YXZB∠XYZC∠YZXD∠ZYX
Find the reflex angle corresponding to each of the following angles:
90∘
View SolutionFind the reference angles corresponding to each of the following angles. It may help if you sketch θ in standard position. θ=−2300 (ii) 31π9 (iii) θ=6400
View SolutionFind the reference angles corresponding to each of the following angles. It may help if you sketch θ in standard position. θ=−230∘ (ii)31π9 (iii)θ=640∘
View SolutionState the kind of each of the following angles:
View SolutionFind the complement of each of the following angles:
View Solution

