Find the value of x in each of the following :
16:x::x:25
The correct Answer is:x = 20
To solve the problem 16:x::x:25, we can follow these steps:
Step 1: Understand the Proportion
The given proportion can be expressed mathematically as:
16x=x25
Step 2: Cross-Multiply
To eliminate the fractions, we cross-multiply:
16⋅25=x⋅x
This simplifies to:
400=x2
Step 3: Solve for x
To find x, we take the square root of both sides:
x=√400
Step 4: Calculate the Square Root
Calculating the square root gives:
x=20
Final Answer
Thus, the value of x is:
20
---
The given proportion can be expressed mathematically as:
16x=x25
To eliminate the fractions, we cross-multiply:
16⋅25=x⋅x
This simplifies to:
400=x2
To find x, we take the square root of both sides:
x=√400
Calculating the square root gives:
x=20
Thus, the value of x is:
20
Topper's Solved these Questions
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Example
20 Videos
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Try This!
29 Videos
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise 7 A
38 Videos
- PROPERTIES OF TRIANGLESBOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18B
10 Videos
- RATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL NUMBERS EXERCISE - REVISION EXERCISE (FILL IN THE BOXES).
4 Videos
Similar Questions
Find the value of x in each of the following :
42 : 12 : : 7 : x
View SolutionFind the value of x in each of the following :
6 : 0.8 : : x : 10
View SolutionFind the value of x in each of the following :
x : 1.6 : : 2.1 : 8.4
View SolutionFind the value of x in each of the following :
1 . 8 : x : : 2 . 4 : 6 . 0
View SolutionFind the value of x in each of the following figures.
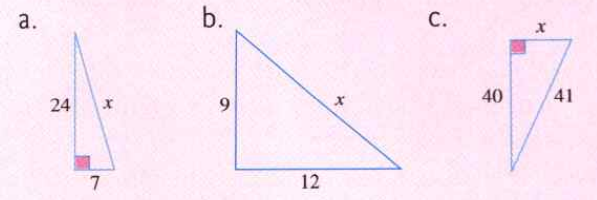
View SolutionFind the value of x in each of the following figures.
View SolutionFind the value of x in each of the following triangles.
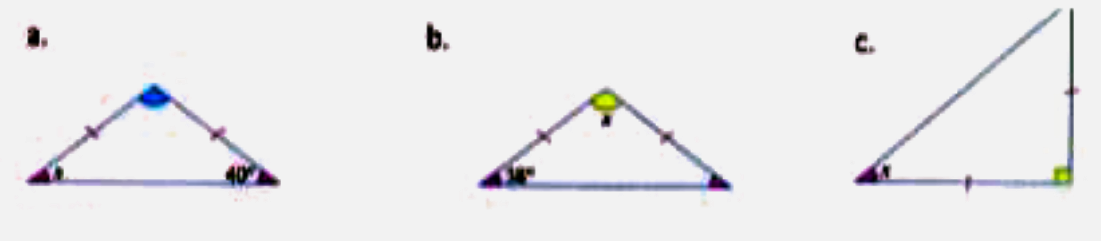
View SolutionFind the value of x in each of the following :
119:x::13:14
View SolutionFind the 'x' in each of the following
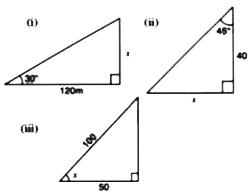
View SolutionFind the value of x in each of the following figures if l∣∣m.
View Solution
