For a set of ungrouped values the following sums are found:
n=15,∑x=480,∑x2=15735.
Find the standard deviation.
The correct Answer is:5
To find the standard deviation for the given ungrouped data, we can use the formula for standard deviation:
σ=
⎷∑x2n−(∑xn)2
Where:
- n is the number of observations,
- ∑x is the sum of the observations,
- ∑x2 is the sum of the squares of the observations.
Given:
- n=15
- ∑x=480
- ∑x2=15735
Step 1: Calculate ∑x2n
First, we calculate ∑x2n:
∑x2n=1573515
Calculating this gives:
1573515=1049
Step 2: Calculate ∑xn
Next, we calculate ∑xn:
∑xn=48015
Calculating this gives:
48015=32
Step 3: Calculate (∑xn)2
Now, we square the result from Step 2:
(∑xn)2=322=1024
Step 4: Substitute values into the standard deviation formula
Now, we substitute the values into the standard deviation formula:
σ=√1049−1024
Calculating this gives:
σ=√25
Step 5: Calculate the final value of standard deviation
Finally, we find the square root:
σ=5
Thus, the standard deviation for the given data is 5.
Summary of Steps:
1. Calculate ∑x2n.
2. Calculate ∑xn.
3. Square the result from Step 2.
4. Substitute into the formula and simplify.
5. Take the square root to find the standard deviation.
⎷∑x2n−(∑xn)2
- n is the number of observations,
- ∑x is the sum of the observations,
- ∑x2 is the sum of the squares of the observations.
- n=15
- ∑x=480
- ∑x2=15735
1. Calculate ∑x2n.
2. Calculate ∑xn.
3. Square the result from Step 2.
4. Substitute into the formula and simplify.
5. Take the square root to find the standard deviation.
Topper's Solved these Questions
- MEASURES OF DISPERSIONBook:ICSEChapter:MEASURES OF DISPERSIONExercise:CHAPTER TEST
Explore 6 Videos
- MEASURES OF DISPERSIONBook:ICSEChapter:MEASURES OF DISPERSIONExercise:EXERCISE 21 (a)
Explore 12 Videos
- MEASURES OF CENTRAL TENDENCYBook:ICSEChapter:MEASURES OF CENTRAL TENDENCYExercise:EXERCISE
Explore 14 Videos
- MOCK TEST PAPER-2021Book:ICSEChapter:MOCK TEST PAPER-2021Exercise:SECTION - C
Explore 10 Videos
Similar Questions
Five students secured marks as, 8, 10, 15, 30, 22. Find the standard deviation.
View SolutionFor a series the information available is n=10∑x=60,∑x2=1000. The standard deviation is
View SolutionFind the standard deviation for the following data

View SolutionFind the standard deviation for the following data

View SolutionFind the standard deviation of the following distribution :
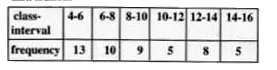
View SolutionThe sum of 10 items is 12 and sum of their squares is 18, then find the standard deviation ?
View SolutionFind the standard deviation from the following data:

View SolutionFind the standard deviation of first n natural numbers.

View SolutionFind the standard deviation from the following datas:
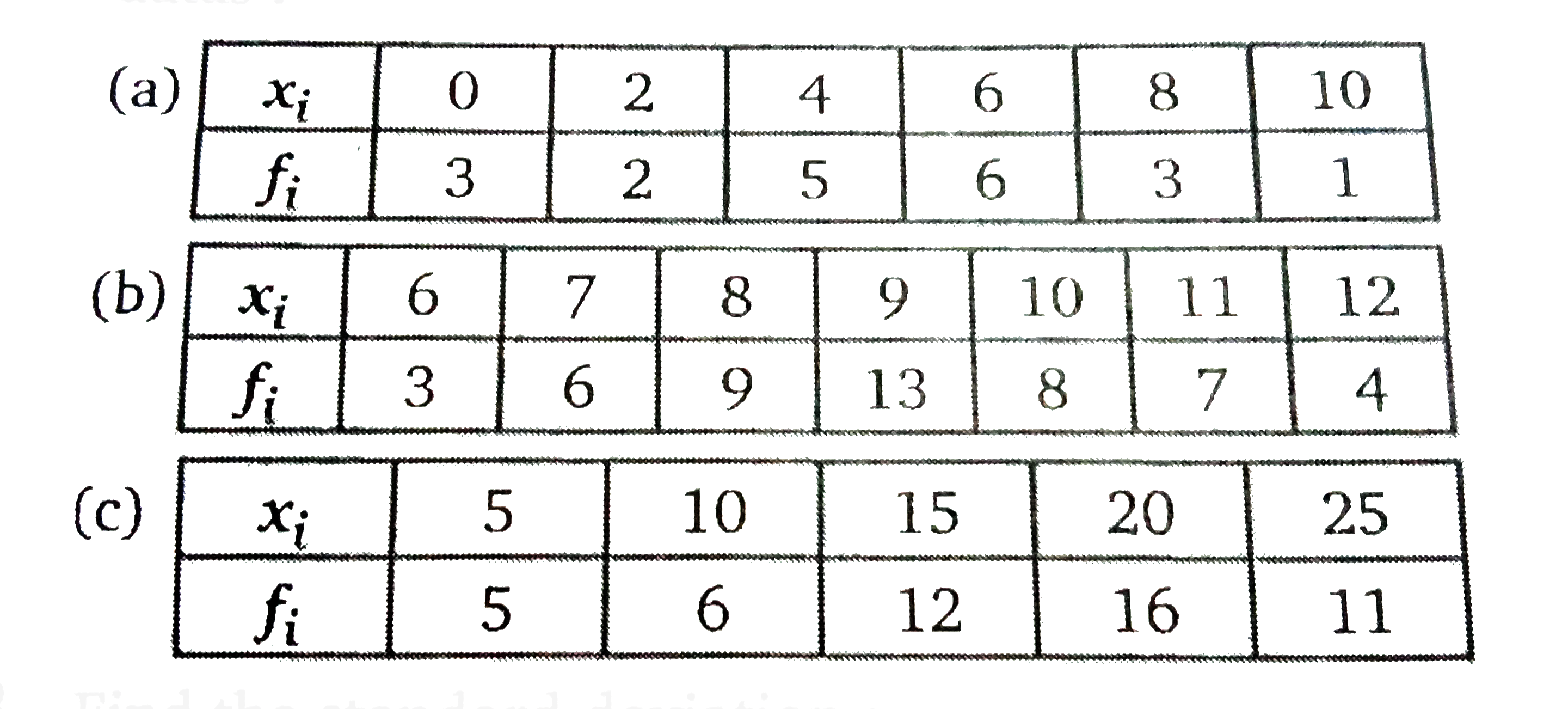
View SolutionFind the values of the following trigonometric ratio: cos(−4800)
View Solution

