The scores of a batsman in ten innings are:
48, 80, 58, 44, 52, 65, 73, 56, 64, 54. Find the mean deviation from the median.
The correct Answer is:8.6
To find the mean deviation from the median for the given scores of a batsman in ten innings, we will follow these steps:
Step 1: Arrange the Scores in Ascending Order
First, we need to arrange the scores in ascending order.
Scores: 48, 80, 58, 44, 52, 65, 73, 56, 64, 54
Ascending Order: 44, 48, 52, 54, 56, 58, 64, 65, 73, 80
Step 2: Find the Median
Since there are 10 scores (an even number), the median will be the average of the 5th and 6th scores in the ordered list.
5th Score: 56
6th Score: 58
Median (M): (56 + 58) / 2 = 114 / 2 = 57
Step 3: Calculate the Mean Deviation from the Median
The mean deviation from the median is calculated using the formula:
Mean Deviation=1nn∑i=1|xi−M|
Where:
- n = number of observations (10)
- xi = each score
- M = median (57)
Step 4: Calculate the Absolute Deviations
Now, we will calculate the absolute deviations from the median for each score:
1. |44 - 57| = 13
2. |48 - 57| = 9
3. |52 - 57| = 5
4. |54 - 57| = 3
5. |56 - 57| = 1
6. |58 - 57| = 1
7. |64 - 57| = 7
8. |65 - 57| = 8
9. |73 - 57| = 16
10. |80 - 57| = 23
Step 5: Sum the Absolute Deviations
Now we will sum all the absolute deviations calculated above:
Total Absolute Deviations=13+9+5+3+1+1+7+8+16+23=86
Step 6: Calculate the Mean Deviation
Now we can calculate the mean deviation:
Mean Deviation=8610=8.6
Final Answer
The mean deviation from the median is 8.6.
---
First, we need to arrange the scores in ascending order.
Ascending Order: 44, 48, 52, 54, 56, 58, 64, 65, 73, 80
Since there are 10 scores (an even number), the median will be the average of the 5th and 6th scores in the ordered list.
6th Score: 58
Median (M): (56 + 58) / 2 = 114 / 2 = 57
The mean deviation from the median is calculated using the formula:
- n = number of observations (10)
- xi = each score
- M = median (57)
Now, we will calculate the absolute deviations from the median for each score:
2. |48 - 57| = 9
3. |52 - 57| = 5
4. |54 - 57| = 3
5. |56 - 57| = 1
6. |58 - 57| = 1
7. |64 - 57| = 7
8. |65 - 57| = 8
9. |73 - 57| = 16
10. |80 - 57| = 23
Now we will sum all the absolute deviations calculated above:
Now we can calculate the mean deviation:
The mean deviation from the median is 8.6.
Topper's Solved these Questions
- MEASURES OF DISPERSIONBook:ICSEChapter:MEASURES OF DISPERSIONExercise:EXERCISE 21 (a)
Explore 12 Videos
- MEASURES OF DISPERSIONBook:ICSEChapter:MEASURES OF DISPERSIONExercise:EXERCISE 21 (b)
Explore 19 Videos
- MEASURES OF CENTRAL TENDENCYBook:ICSEChapter:MEASURES OF CENTRAL TENDENCYExercise:EXERCISE
Explore 14 Videos
- MOCK TEST PAPER-2021Book:ICSEChapter:MOCK TEST PAPER-2021Exercise:SECTION - C
Explore 10 Videos
Similar Questions
The scores of a batsman in ten innings are : 38,70,48,34,42,55,63,46,54,44. Find the mean deviation about the median.
View SolutionThe scores of a batsman in ten innings are : 38,70,48,34,42,55,63,46,54,44. Find the mean deviation about the median.
View SolutionThe scores of a batsman in ten innings are : 38,70,48,34,42,55,63,46,54,44. Find the mean deviation about the median.
View SolutionRuns scored by a batsman in 10 innings are : 38, 70,48,34,42,55,63,46,54,44
The mean deviation about median is
View SolutionThe marks of 10 students in a class are 38, 70, 48,34 ,42, 55 63, 46, 54,44. Find the standard deviation of these marks.
View SolutionFind the mean deviation from the median for the following data:
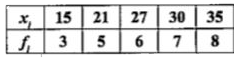
View SolutionThe weights of 13 students (in kg) are :
48, 41, 52, 65, 40, 53, 34, 61, 47, 42, 44, 31, 35
Find the median weight.
View SolutionA batsman scores run in 10 innings as 38,70,48,34,42,55,63,46,54 and 44. The mean deviation about mean is (a) 8.6 (b) 6.4 (c) 10.6 (d) 7.6
View SolutionA batsman scores run in 10 innings as 38,70,48,34,42,55,63,46,54 and 44. The mean deviation about mean is 8.6 (b) 6.4 (c) 10.6 (d) 7.6
View SolutionA cricketer scores the following runs in eight innings:58, 76, 40, 35, 46, 45, 0, 100.Find the mean score.
View Solution