The number of ways in which 9 identical balls can be placed in three identical boxes is
12
6
9
9!3!
The correct Answer is:A
Step by step video, text & image solution for The number of ways in which 9 identical balls can be placed in three identical boxes is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The number of ways in which n distinct balls can be put into three boxes, is
A3nBn3C3nDn+3The number of ways in which n distinct objects can be put into two identical boxes so that no box remains empty, is
A2n−2B2n−1C2n−1−1D2n−1If number of ways in which 7 identical balls can be distributed into 4 boxes, so that no box remains empty is 4λ, the value of λ is
A5B7C9D11
Find the number of ways in which 5 distinct balls can be distributed in three different boxes if no box remains empty.
View SolutionFind the number of ways in which n distinct objects can be kept into two identical boxes that no box remains empty.
View SolutionIn the given figure, what is the maximum number of different ways in which 8 identical balls can be placed in the small triangles 1, 2, 3 and 4 such that each triangle contains at least one ball?
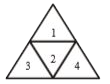
View SolutionNumber of ways in which 6 distinct objects can be kept into two identical boxes so that no box remains empty is
View SolutionThe number of ways in which 10 balls can be selected from 10 identical green balls, 10 identical blue balls and 9 idenitcal red balls are
View Solution
