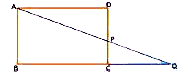
Find the area of the rectangle ABCD, if P is any point on AB such that DP = 18 mm, CP = 21 mm and ∠DPC=90∘.
378mm2
189mm2
126mm2
136mm2
The correct Answer is:A
To find the area of rectangle ABCD given the conditions in the problem, we can follow these steps:
Step 1: Understand the Geometry
We have rectangle ABCD with point P on side AB. We know that:
- DP = 18 mm
- CP = 21 mm
- Angle DPC = 90°
Step 2: Identify Triangle DPC
Since angle DPC is 90°, triangle DPC is a right triangle. We can use the formula for the area of a triangle:
Area of triangle=12×base×height
Here, we can consider DP as the base and CP as the height.
Step 3: Calculate the Area of Triangle DPC
Substituting the values:
- Base (DP) = 18 mm
- Height (CP) = 21 mm
The area of triangle DPC is:
Area of triangle DPC=12×18mm×21mm
Calculating this:
=12×378mm2=189mm2
Step 4: Relate the Area of Triangle DPC to Rectangle ABCD
Since triangle DPC shares the same base (DP) and height (CP) with rectangle ABCD, we can use the relationship between the area of the triangle and the area of the rectangle. The area of the triangle is half of the area of the rectangle:
Area of triangle DPC=12×Area of rectangle ABCD
Step 5: Solve for the Area of Rectangle ABCD
Let the area of rectangle ABCD be A:
189mm2=12A
Multiplying both sides by 2 to solve for A:
A=189mm2×2=378mm2
Conclusion
The area of rectangle ABCD is:
Area of rectangle ABCD=378mm2
We have rectangle ABCD with point P on side AB. We know that:
- DP = 18 mm
- CP = 21 mm
- Angle DPC = 90°
Since angle DPC is 90°, triangle DPC is a right triangle. We can use the formula for the area of a triangle:
Area of triangle=12×base×height
Here, we can consider DP as the base and CP as the height.
Substituting the values:
- Base (DP) = 18 mm
- Height (CP) = 21 mm
Area of triangle DPC=12×18mm×21mm
Calculating this:
=12×378mm2=189mm2
Since triangle DPC shares the same base (DP) and height (CP) with rectangle ABCD, we can use the relationship between the area of the triangle and the area of the rectangle. The area of the triangle is half of the area of the rectangle:
Area of triangle DPC=12×Area of rectangle ABCD
Let the area of rectangle ABCD be A:
189mm2=12A
Multiplying both sides by 2 to solve for A:
A=189mm2×2=378mm2
The area of rectangle ABCD is:
Area of rectangle ABCD=378mm2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a rectangle ABCD , E is the mid -point of AB . If AB= 16 m and AD = 6 m , then find ED .
A15 cmB10 cmC12 mD14 mIn parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC
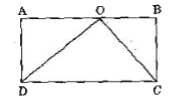
In the figure given above, the area of rectangle ABCD is 100 square cm, O is any point on AB and CD = 20 cm. Then the area of triangle COD ia
View SolutionFind the area of a square whose side is 63mm.
View SolutionFind the area of a rectangle if its length and breadth are 28cm and 120mm, respectively.
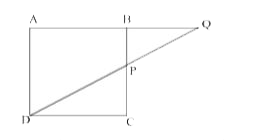
View SolutionIn the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
View SolutionThe area of any parallelogram ABCD, is AB X BC.
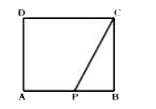
View SolutionABCD is a rectangle. P is a point on the side AB as shown in the given figure. If DP = 13, CP = 10 and BP = 6, then what is the value of AP?
View Solution