In a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. The number of people who like the three sweets
12
6
8
none of these
The correct Answer is:A
To solve the problem step by step, we will use the information given and set up equations based on the relationships described.
Step 1: Define Variables
Let:
- F = Number of people who like all three sweets (Barfi, Jalebi, Rasgulla)
- D = Number of people who like exactly Barfi and Jalebi
- E = Number of people who like exactly Barfi and Rasgulla
- G = Number of people who like exactly Jalebi and Rasgulla
Step 2: Set Up Equations
From the problem, we know:
1. The number of people who like all three sweets is half the number of people who like exactly two sweets:
F=12(D+E+G)
2. The number of people who like exactly any two out of the three sweets is the same:
D=E=G
Let D=E=G=d. Thus, we can rewrite the first equation:
F=12(d+d+d)=3d2
Step 3: Total People Who Like Each Sweet
We are given:
- People who like Barfi = 50
- People who like Jalebi = 60
- People who like Rasgulla = 70
Using the principle of inclusion-exclusion, we can express the total number of people who like each sweet:
1. For Barfi:
50=B+D+E+F
Substituting E and D with d:
50=B+d+d+F⟹50=B+2d+F
2. For Jalebi:
60=J+D+G+F⟹60=J+d+d+F⟹60=J+2d+F
3. For Rasgulla:
70=R+E+G+F⟹70=R+d+d+F⟹70=R+2d+F
Step 4: Summing the Equations
Now, we can add the three equations:
(50+60+70)=(B+J+R)+3d+3F
This simplifies to:
180=(B+J+R)+3d+3F
Step 5: Total Number of People
We also know the total number of people is 132:
132=B+J+R+D+E+F+G=B+J+R+3d+F
Step 6: Solve the Equations
Now we have two equations:
1. 180=(B+J+R)+3d+3F
2. 132=(B+J+R)+3d+F
Subtract the second equation from the first:
180−132=3F−F⟹48=2F⟹F=24
Step 7: Find d
Now substitute F back into the equation for F:
F=3d2⟹24=3d2⟹3d=48⟹d=16
Conclusion
The number of people who like all three sweets (Barfi, Jalebi, Rasgulla) is:
24
Let:
- F = Number of people who like all three sweets (Barfi, Jalebi, Rasgulla)
- D = Number of people who like exactly Barfi and Jalebi
- E = Number of people who like exactly Barfi and Rasgulla
- G = Number of people who like exactly Jalebi and Rasgulla
From the problem, we know:
1. The number of people who like all three sweets is half the number of people who like exactly two sweets:
F=12(D+E+G)
D=E=G
Let D=E=G=d. Thus, we can rewrite the first equation:
F=12(d+d+d)=3d2
We are given:
- People who like Barfi = 50
- People who like Jalebi = 60
- People who like Rasgulla = 70
1. For Barfi:
50=B+D+E+F
Substituting E and D with d:
50=B+d+d+F⟹50=B+2d+F
60=J+D+G+F⟹60=J+d+d+F⟹60=J+2d+F
70=R+E+G+F⟹70=R+d+d+F⟹70=R+2d+F
Now, we can add the three equations:
(50+60+70)=(B+J+R)+3d+3F
This simplifies to:
180=(B+J+R)+3d+3F
We also know the total number of people is 132:
132=B+J+R+D+E+F+G=B+J+R+3d+F
Now we have two equations:
1. 180=(B+J+R)+3d+3F
2. 132=(B+J+R)+3d+F
180−132=3F−F⟹48=2F⟹F=24
Now substitute F back into the equation for F:
F=3d2⟹24=3d2⟹3d=48⟹d=16
The number of people who like all three sweets (Barfi, Jalebi, Rasgulla) is:
24
Topper's Solved these Questions
Similar Questions
In a group of persons , the number of persons who like only tea is half that of those who like only coffe , or one -third of that of those who like neither tea nor coffee, or one - fourth of that of those who like both tea and coffee . If there are 100 persons in the group , then find the number of persons who like both tea and coffee.
View SolutionIn a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. The number of people who like the three sweets
View Solution
Knowledge Check
In a group of 132 people 50, 60, 70 people like three different sweets-Barfi, Jalebi, Rasgulla, respectively. The number of people who like all the three sweets is half the number of people who like exactly two sweets. The number of people who like exactly any two out of the three sweets is the same as those who like exactly any other two of the three sweets. The number of people who like the three sweets
A12B6C8Dnone of theseFind out the number of people who do not play any game.
 A9B18C15D24
A9B18C15D24The pie chart given below shows the distribution of students who like the given 5 sports. The total number of students is 960.
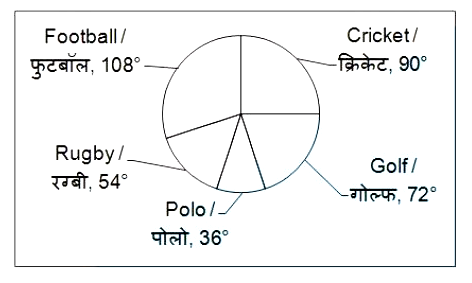
The total number of students who like these 2 sports is equal to the number of students who like Cricket. Which are these 2 sports?A269B300C231D369
Children like to eat sweets, isn't it?
View SolutionWhat is the respective ratio of the number of teachers who teach Mathematics and the number of teach- ers who teach Hindi? ?

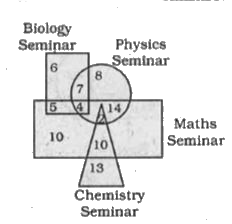
View SolutionThe Venn diagram below shows the number of people who attended seminars on Physics , Chemistry . Maths and Biology . What is the number of people who attended exactly any two seminars ?
View SolutionPeople are more likely to be healthy if-
View SolutionA marketing company conducted a survey among 10,000 person in Kanpur :
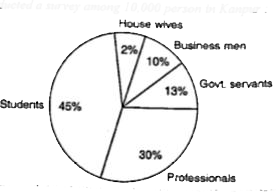
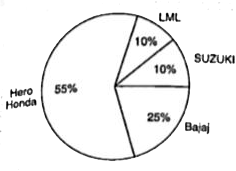
It was observed that some people have more than one bike but from only one company i.e., a particular person can have more than one bike of HeroHonda, but not from bajaj etc. and vice versa. Thus there were total 12,000 bikes with 10,000 persons used for survey. There are only four compaies operating in this market.
If the number of people who drive one, two and three bikes are in the ratio 15 : 3 : 1 what is the number of people in the survey who do not drive even a single bike ?
View Solution
